Введем вектор г - Р - Q. Тогда \Т(Р) - T(Q)\ = \Мт\ = \(rxmn + ryml2, глт21 + гут22)\. Равенство выражений |Мг|2 и |г|2 требует, чтобы выполнялись соотношения m2 + m2( = 1, т\2 + mW - 1, mnml2 + т22т21 - 0, что и требовалось доказать.
5.8.7. Эллипсы инвариантны
Докажите, что эллипсы инвариантны относительно аффинного преобразования. Это означает, что если Е- эллипс, а Г - аффинное преобразование, то образ Т(Е) из точек эллипса £ также является эллипсом. Ключ к решению
Любое аффинное преобразование является комбинацией из поворотов и масштабирований. Очевидно, что после поворота эллипс остается эллипсом, поэтому испортить этот эллипс могут только нерав-. номерные масштабирования. Поэтому достаточно доказать, что эллипс, подвергнутый неравномерному масштабированию, остается эллипсом.
Преобразования объектов
5.8.8. Другие инвариантные формы
Рассмотрим, какой класс форм (возможно, более широкий, чем эллипсы) является инвариантным относительно аффинных преобразований. В предположении, что некоторая форма описывается уравнением f(x, у) = 0, докажите, что после преобразования Т новая форма описывается множеством всех точек, удовлетворяющих уравнению g(x, у) =f(T'l(x, у)) = 0. После этого опишите детали этой формы в случае, когда Т- аффинное преобразование. И, наконец, попробуйте описать наиболее общий класс форм, сохраняющихся под воздействием аффинных преобразований.
Тематическое задание 5.4. Обобщенные трехмерные сдвиги Уровень сложности II
Сдвиг может иметь более общий вид, чем тот, который рассматривался в разделе «Элементарные трехмерные преобразования». Как предложил Голдман [Goldman, 84], сдвиг состоит из: О плоскости, проходящей через начало координат и имеющей единичную нормаль т; О единичного вектора v, лежащего в этой плоскости (и поэтому перпендикулярного вектору т); О угла0.
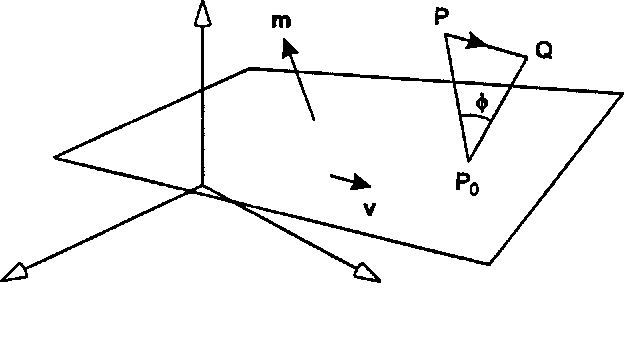
Рис. 5.59. Определение трехмерного сдвига Тогда, как показано на рис. 5.59, сдвиг точки Р в точку () осуществляется посредством ее перемещения на нужную величину в направлении V. Эта величина пропорциональна расстоянию, на которое точка Р отстоит от плоскости, а также тангенсу угла ф. Голдман доказал, что такой сдвиг имеет следующее матричное представление"opengl1_375.html">⇐ Предыдущая| |Следующая ⇒
