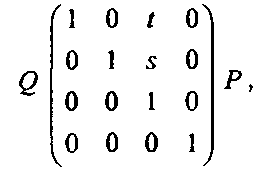
(5.47)под действием которого трехмерная точка Р сдвигается вдоль оси х, отдаляясь от оси 2 на величину I, и вдоль оси у, отдаляясь от той же оси 2 на величину 5. Докажите, что точка Р, расположенная в плоскости г = 1 и имеющая координаты Р = (Рх, Р, 1), преобразуется в точку (Рх + г, Ру + я, 1). Иными словами, эта точка просто перемещается вдоль оси х на величину г и вдоль оси у на величину 5. Докажите также, что для произвольной точки в плоскости 2=1 такой сдвиг эквивалентен перемещению. И, наконец, докажите, что левый верхний минор размерностью три на три, вырезанный из матрицы (5.47), идентичен формуле чистого двумерного перемещения в однородных координатах. Осознание этой идентичности углубит понимание того, как работают однородные координаты.
Преобразования объектов
Тематическое задание 5.5. Вращение вокруг оси: конструктивный подход Уровень сложности И.
В данном тематическом задании вас попросят заполнить пробелы в выводе уравнения (5.33) для матрицы поворота J?u(ß). Примем для простоты, что вектор и является ортом: |и| - 1. Обозначим через р радиус-вектор, заканчивающийся точкой Р, так что р - Р - О, где О - начало данной системы координат. Теперь спроектируем вектор р на вектор и для получения вектора h, как показано на рис. 5.29, а.
а) Докажите, что вектор h имеет форму (р u)u. Определите два перпендикулярных вектора а - р - h и b - и а, лежащие в плоскости поворота.
б) Докажите, что векторы а и Ь взаимно перпендикулярны, имеют одинаковую длину, оба расположены в плоскости вращения, а также что выражение b - и (р - h) можно упростить до и р. Таким методом можно эффективно задавать двумерную систему координат в плоскости вращения. Посмотрите теперь на плоскость вращения, приведенную на рис. 5.29, б. Операция поворота поворачивает вектор а в а' - acosß + bsinß, следовательно, повернутая точка имеет вид:
Q - h + acosß + bsinß,или, используя вышеприведенные выражения для векторов а и Ь, получаем:
Q - pcosß + ( 1 - cosß)(p u)u + sinß (u x p). (5.48)