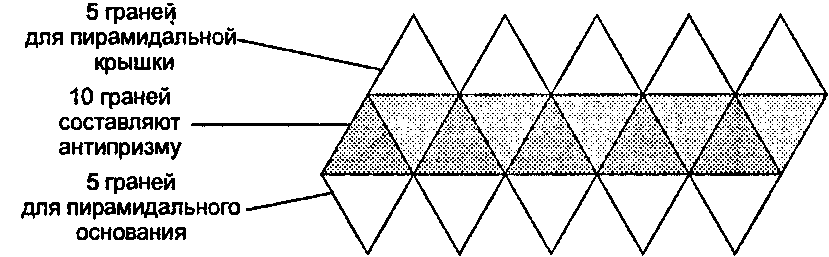
Рис. 6.23. Икосаэдр является антипризмой с крышкой и основанием Додекаэдр

Додекаэдр является двойственным к икосаэдру, поэтому вся информация, необходимая для построения списков для додекаэдра, закдючена в списках для икосаэдра. Однако удобнее рассматривать его модель в «лежачем» положении, как на рис. 6.24.

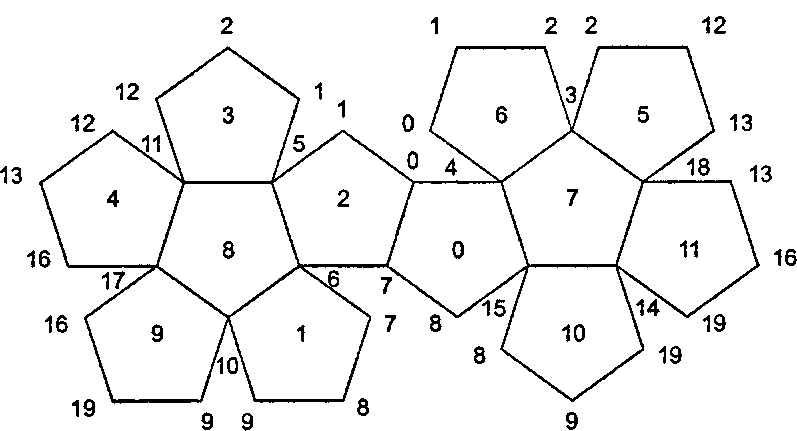
Рис. 6.24. Модель додекаэдра Снова используем двойственность"images/tmp8E4A-381.png" alt="Усеченный куб">

Рис. 6.25. Усеченный куб Например, изображенный на рис. 6.25, а «усеченный куб» имеет в качестве граней 8-угольники и 3-угольники, причем вокруг каждой вершины расположены один треугольник и два восьмиугольника. Эти два свойства данного тела описываются символом 3-8-8.

Усеченный куб сформирован путем «срезания» каждого угла куба под одним и тем же углом. Модель усеченного куба, показанная на рис. 6.25, б, получена из модели основного куба. Каждое ребро куба разделено на три части, средняя из которых имеет длину А = l/(l + V2~) (рис. 6.25, в), и средняя часть каждого ребра соединена со средними частями соседних ребер. Таким образом, если концевые точки ребра куба равны С и Д то две дополнительные вершины, V и W, могут быть получены с помощью аффинных комбинаций"opengl1_402.html">⇐ Предыдущая| |Следующая ⇒