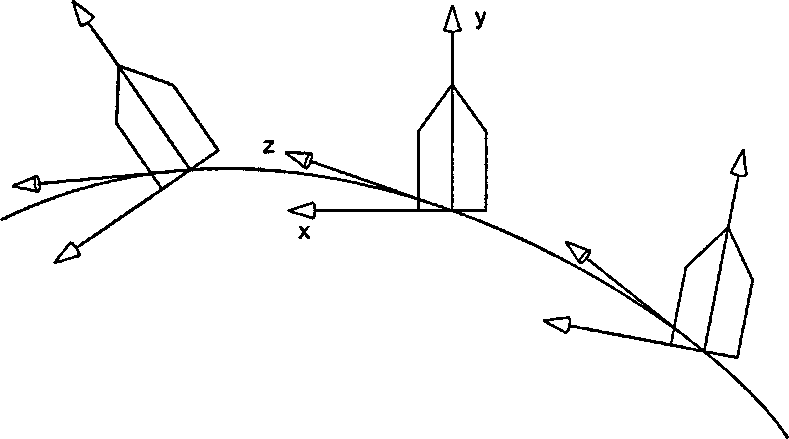
Рис. 6.37. Создание локальных систем координат вдоль хребтовой кривой Когда базис Френе вычислен, нетрудно найти матрицу преобразования М, которая переводит полигон основания трубки в его новую позицию и ориентацию в данном базисе. Эта матрица преобразования переводит мировую систему координат в новую систему. (Приводимые здесь рассуждения напоминают те, которые использовались в практическом упражнении 5.6.1 при преобразовании системы координат камеры в мировую систему координат.) Матрица М. должна переводить векторы i, j, к соответственно в векторы N(t), B(t), Т(г.) и должна перемещать начало координат из мировой точки в точку хребта С(г.). Поэтому матрица содержит столбцы, представляющие собой векторы N(r.), B(cj), Т(г.) и точку C(tt), выраженные в однородных координатах"opengl1_411.html">⇐ Предыдущая| |Следующая ⇒