2. Подставить вместо х, у, г известные функции Х(и, ь), У(и, ь), 2{и, V). Этот способ будет проиллюстрирован в некоторых из последующих примеров.
6.5.3. Влияние аффинного преобразования Иногда нам придется работать с неявной и параметрической формами задания поверхности после того, как эта поверхность подверглась аффинному преобразованию. Нам также понадобится узнать, какое воздействие аффинное преобразование оказывает на нормаль.
Пусть это преобразование представлено в виде матрицы М размерностью четыре на четыре, а исходная поверхность задана в неявной форме (в терминах точек в однородных координатах) F (р) и в парамет-
Моделирование поверхностей полигональными сетками
рической форме Р(и,и) = (Х(и,ь),¥(и,ь)^(и,и)Л)т. Тогда параметрическая форма преобразованной поверхности, очевидно, примет вид МР(и,ь). (Почему?) Также нетрудно показать (см. ниже приведенные упражнения), что неявная форма преобразованной поверхности имеет вид:
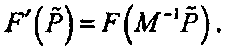
Далее, если исходная поверхность имеет нормальный вектор п(и, v), то преобразованная поверхность будет иметь нормаль, равную М'тп(и, v).
Предположим для примера, что мы преобразуем описанную выше плоскость, заданную уравнением f(P\ = n-P, где n-{nx,ny,nz,-Dy Преобразованная плоскость будет иметь следующую неявную форму: г'(Р} = п-(м~1Р\. Последнее выражение можно записать (см. упражнения ниже) в виде [м~тп)-Р, так что нормальный вектор преобразованной плоскости включает в себя обратную транспонированную матрицу, что согласуется с формулой для нормали к поверхности общего вида.
Практические упражнения
6.5.1. Неявная форма преобразованной поверхности Предположим, что все точки поверхности удовлетворяют уравнению f(p) = 0, а матрица M преобразует Р в Q, то есть Q = МР. Докажите, что любая точка Q преобразованной поверхности соответствует точке m~'q и что все такие точки удовлетворяют уравнению f\m~xq} - 0. Далее покажите, что из этого утверждения следует, что неявная форма преобразованной поверхности имеет вид f (g) = f(m~'Q^ .
6.5.2. Как изменяются нормальные векторы?
