Для получения долек нам необходимо nSlice значений и в диапазоне от 0 до 2я. Обычно эти значения выбираются с постоянным шагом: и, - 2ro'/nSl i ce, i - 0,1.....nSl i ce - 1. Что же касается слоев, то мы

выбираем половину из них над экватором, а половину - под ним. Верхний и нижний слои будут состоять из треугольников, а все остальные - из четырехугольников. Это означает, что мы должны задать (nStacks + 1) широты: vi = п/2 - 7r//nStacks, где] = 0,1.....nStacks.

Теперь можно создавать список вершин. На рисунке показано, как можно нумеровать вершины (порядок нумерации - это дело удобства): северный полюс помещаем в pt[0], нижние точки верхних слоев-в следующие 12 вершин и т. д. При 12 дольках и 8 ломтиках всего будет 98 точек. (Почему?)

6.5. Каркасные аппроксимации гладких объектов

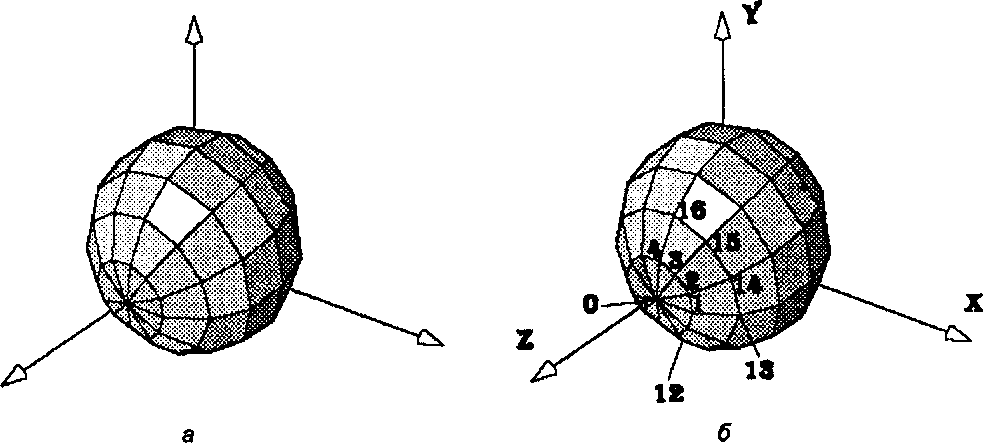
Рис. 6.49. Каркасная аппроксимация базовой сферы (а); нумерация вершин (5)

Столь же легко может быть создан список нормалей"opengl1_427.html">⇐ Предыдущая| |Следующая ⇒