Однополостный гиперболоид. Если а - Ъ, то такой гиперболоид становится поверхностью вращения, образованной посредством вращения гиперболы вокруг оси. Главные следы для плоскостей г = к являются эллипсами, а для плоскостей x"kny"k- гиперболами. Однополостный гиперболоид особенно интересен тем, что он является линейчатой поверхностью, как показано на рис. 6.62, а. Такая поверхность может получиться, если переплести нитью два параллельных эллипса так, как показано на рисунке. Формулы для образующих «нитей» рассматриваются в упражнениях.

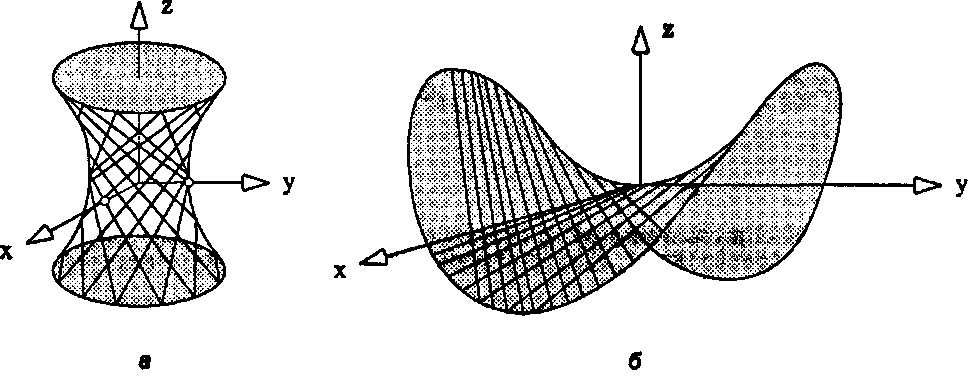
Рис. 6.62. Две линейчатые поверхности второго порядка Двуполостный гиперболоид. В диапазоне от х = -а до д"opengl1_439.html">⇐ Предыдущая| |Следующая ⇒