Р(и, о)-(«,/(«,»), о), (6.49)
а их нормальный вектор имеет следующий вид:
(Проверьте это.)
Следовательно, величины и и V могут быть непосредственно использованы в качестве зависимых переменных для данной функции. Поэтому и-контуры располагаются в плоскостях с постоянным х, а я-кон б.б. Заключение туры - в плоскостях с постоянным 2. На рис. 6.66, а показана поверхность, описываемая уравнением (6.47), а на рис. 6.66, б - уравнением (6.48). Каждая линия является следом пересечения поверхности плоскостью х " к или 2 - к при некотором значении к. Подобные рисунки могут помочь при иллюстрации поведения математической функции.
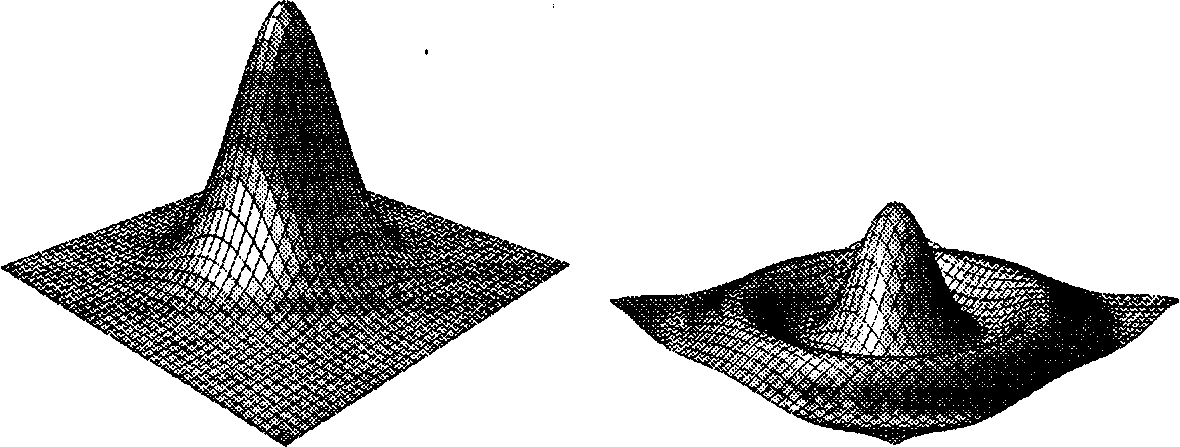
а б Рис. 6.66. Два поля высот: а) гауссиана; б) гармоническая sinc-функция Практическое упражнение 6.5.32. Квадрики как явные функции Эллиптический параболоид можно записать в виде функции г- fix, у), тогда его параметрическая форма будет иметь вид: (и, v,f(u, v)). Чему равна функция /( )? В каких случаях удобна такая форма записи? Какие другие квадрики могут быть представлены таким способом? Можно ли написать аналогичные явные представления для каких-нибудь суперквадрик?
6.6. Заключение Эта глава посвящена моделированию и рисованию разнообразных поверхностей трехмерных объектов. Для осуществления этого нужно находить математические описания поверхностей различных форм и создавать эффективные структуры данных, в которых содержится описание поверхности, достаточно подробное для ее визуализации. Мы разработали класс Mesh (сетка), поля данных которого содержат три списка: список вершин, список нормалей и список граней. Такая структура может эффективно сохранять все необходимые геометрические данные об объектах с плоскими гранями, такими как многогранник; и может хранить данные, достаточные для моделирования полигональной «оболочки», аппроксимирующей гладкие криволинейные поверхности.
Мы показали, что когда структура данных для сетки построена, ее нетрудно визуализировать в программной среде OpenGL. Столь же просто записать данные о сетке в файл и считывать его в программу. Современные алгоритмы закрашивания используют нормальный вектор в каждой вершине каждой грани, чтобы можно было определить, насколько светлыми или темными должны быть изображены различные точки грани. Если грань должна быть нарисована плоской, то для каждой вершины используется один и тот же нормальный вектор, а именно вектор, нормальный к самой этой грани. Если сетка создается для приближенного представления гладкой криволинейной поверхности, то нормальный вектор в каждой вершине полагается равным нормали к истинной поверхности в этой точке, а алгоритмы визуализации для передачи плавно изменяющихся теней изображения используют формулу интерпо-
