Далее рассмотрим проекцию треугольника Г на плоскость с нормальным вектором п. Эта проекция Ґ задается проекциями векторов у'и^а его площадь составляет Area(7") =l/2|w' х v'|, откуда V х = 2 Агеа(Г) п. Теперь вычислим w' и v' и найдем выражение для Area (Г').
6.7. Тематические задания
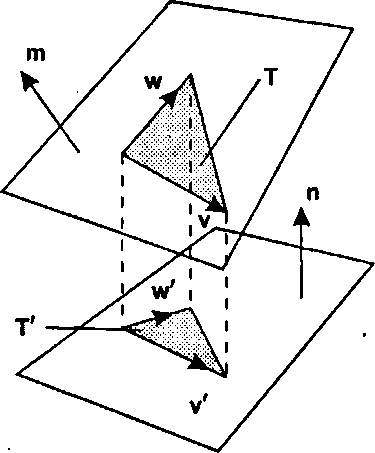
Рис. 6.68. Влияние ортогональной проекции на площадь
2. Используя идеи главы 4, покажите, что вектор v проецируется в вектор v' = v - (v n) n и что, аналогично, w' = w - (w n) п.
Таким образом, задача сводится к сравнению длин двух векторных произведений.
3. С помощью формул для v'hV докажите, что
v' х w' = v х w - (w n) (v x n) + (v n) (w x n) + (w n) (v n) (n x n) и объясните, почему
последний член равен нулю. Тогда получим"opengl1_448.html">⇐ Предыдущая| |Следующая ⇒
