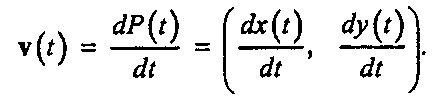
(11.1)

Например, в любой момент времени t эллипс, определяемый уравнением F(t) = (vvcos(c), Wsin(c)), имеет скорость v(t) - (- Wsin(t), Hcos(t)). Длину вектора v(c) часто называют величиной скорости (speed) в момент t. На рис. 11.2 показан вектор скорости в нескольких точках вдоль эллипса. При изменении времени t меняются как величина, так и направление скорости v. (В каком месте скорость наибольшая?)

Выражение для касательной (tangent line) к кривой P(t) в момент t - ta можно получить в параметрической форме L(u), причем параметр и означает следующее: очевидно, что касательная проходит через точку P(ta) «при» и - 0 и «движется» в направлении v(£0). Поэтому уравнение касательной имеет следующий вид:

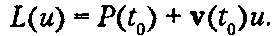
(11.2)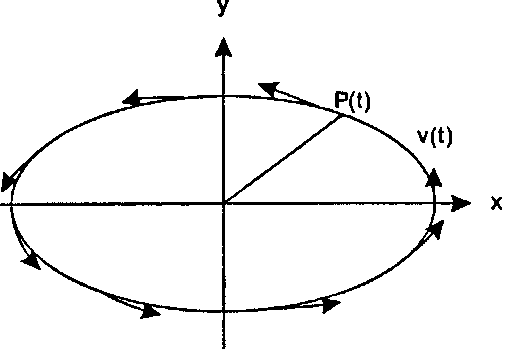

Рис. 11.2. Скорость функции P(t) вдоль кривой

Создание кривых и поверхностей

Эта формула дает возможность легко вычислять и строить касательные к кривым в различных приложениях.

Нормальное (normal) направление к кривой также может быть найдено в каждой точке. Нормаль определяется как направление, перпендикулярное к касательной в интересующей нас точке. Тогда, если касательная в момент ta имеет направление v(t0), то нормальное направление в этот же момент t0 будет пропорционально вектору

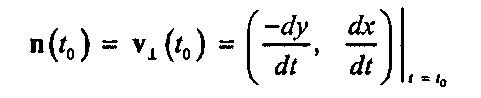
Например, у эллипса, заданного функцией P(t), нормальный вектор равен (-Hcos(t), - Ws'm(t)) или пропорционален этой величине. В частном случае окружности нормаль n(t) пропорциональна самой функции P(t), поэтому направление нормали совпадает с направлением радиус-вектора, соединяющего О с точкой P(t). (Отметим, что для эллипса это не так.)

Когда кривая P(t) используется для описания движения во времени такого объекта, как камера, то возникает следующий вопрос"opengl1_757.html">⇐ Предыдущая| |Следующая ⇒