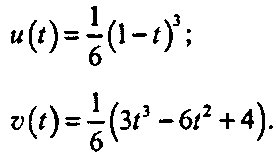
(11.65)11.7. Базисные функции В-сплайнов Непосредственное вычисление производных показывает, что первая и вторая производные кубического сплайна непрерывны повсюду, поэтому кубические сплайн-кривые являются 2-гладкими, по крайней мере, для равноотстоящих узлов.
Основываясь на вышеприведенных рассуждениях, можно показать (см. упражнения) в общем виде, что функция Nk m(t) начинается в точке tk и заканчивается в точке +т, поэтому ее поддержка равна [tk, tt + J. Кроме того, данная функция всюду неотрицательна.
Всегда следует предусмотреть потенциальную возможность деления на нуль: один из знаменателей в уравнении (11.58) или оба сразу могут обратиться в нуль при определенном выборе узлов. Однако если такое и произойдет, то соответствующая функция более низкого порядка, Nkm_ ,(с) или Nk+, т_ ,(£), всегда тоже обратится в нуль. Поэтому можно ввести правило, согласно которому любой член с нулевым знаменателем полагается равным нулю.
Рекурсивную формулу для функции Nt m(c) легко реализовать на компьютере и тем самым получить возможность вычислять ее значение для любого с и для любого заданного узлового вектора. Фрагмент этого кода, приведенный в листинге 11.1, является непосредственным переводом уравнения (11.58).
Листинг 11.1. Вычисление стыковочных функций В-сплайна
float bSplineCint k. int m, float t. float knot[]) {
float denoml. denom2. sum - 0.0: if(m - 1)return (t >- knot[k] && t < knot[k+l]): // 1 or 0 // 1 или 0
// m exceeds 1.. use recursion // если m больше 1. то используем рекурсию denoml - knot[k + m -1] - knot[k]: if(denoml !- 0.0)
sum - (t - knot[k]) * bSpline(k.m-l.t. knot) / denoml: denom2 - knot[k + m] - knot[k+l]; if(denom2 !- 0.0)
sum +- (knot[k+m] - t) * bSpline(k+l,m-l,t,knot) / denom2: return sum;
}Практические упражнения
11.7.1. Потенциальное деление на нуль
Покажите, что если два узла имеют одно и то же значение, то знаменатель в уравнении (11.58) обращается в нуль. Покажите далее, что в этом случае член с нулевым знаменателем также равен нулю.
