У дизайнера уже есть один способ осуществить интерполяцию: использование В-сплайнов; если задать контрольные точки достаточной кратности, то В-сплайн кривая будет заведомо интерполировать эти точки. В тематическом задании 11.6 мы познакомимся с другим методом, основанным на В-сплай-нах. Согласно этому методу, дизайнер задает точки, а алгоритм вычисляет другой набор точек, такой, что В-сплайн кривая, сгенерированная по этим точкам, пройдет через точки, заданные дизайнером.

В данном разделе мы вкратце рассмотрим такие алгоритмы генерирования кривых, которые непосредственно интерполируют все контрольные точки, задаваемые пользователем. Это обширная тема с длинной историей, поэтому мы коснемся только ограниченного класса методов. В работе Фарина [Farin, 60] интерполяция рассматривается в более общей постановке и более подробно.

11.10.1. Интерполяция посредством кусочных кубических полиномов Ниже будет описана интерполяция набора контрольных точек с использованием кусочных кубических полиномов. Мы сознательно ограничиваемся кусочными кубическими полиномами, поскольку они обладают достаточными для наших нужд возможностями и гибкостью и в то же время достаточно просты для эффективного использования.

На рис. 11.39, а приведена основная задача проектирования. Пользователь размещает последовательность контрольных точек Р0, Р,,…, PL (здесь L = 4) и хочет сгенерировать «достаточно гладкую» кривую, проходящую поочередно через все эти точки. На рис. 11.39, б показана одна такая кривая R(t).

24 Ф. Хилл

Создание кривых и поверхностей

Эта кривая состоит из четырех сегментов (участков), каждый из которых является кубическим полиномом:

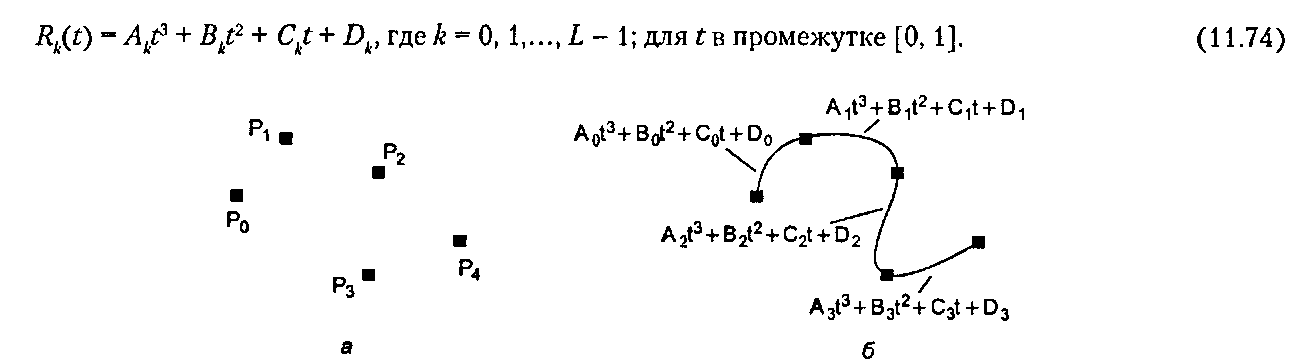
Рис. 11.39. Интерполяция кусочными кубическими полиномами Разумеется, каждый член этого полинома содержит*- и г/-компоненты. Вопрос заключается в следующем"opengl1_807.html">⇐ Предыдущая| |Следующая ⇒