Дополнительное задание 3. Преобразования В-сплайн кривых. Расширьте свою программу так, чтобы пользователь мог задать аффинное преобразование (возможно, из заранее составленного списка), а также контрольный полигон, после чего на базе преобразованного полигона должна рисоваться В-сплайн кривая.

Тематическое задание 11.6. Интерполяция контрольных точек В-сплайнами Уровень сложности III.

Кривая на базе В-сплайн стыковочных функций и стандартного узлового вектора интерполирует только первую и последнюю контрольные точки. Можно, однако, предварительно обработать контрольные точки так, чтобы В-сплайн кривая интерполировала каждую из них. При этой предварительной обработке из заданного набора контрольных точек создается новый их набор. Особенность этого нового набора заключается в том, что сформированная на его базе В-сплайн кривая проходит через все точки исходного набора.

Рассмотрим основную идею этого метода на конкретном примере: совокупность из шести заданных точек у0.....у5 для равноотстоящих значении г интерполируется кубическими В-сплайнами, как показано на рис. 11.65, а. Вместо применения стандартного узлового вектора узлы сделаны равноотстоящими, так что функция Л^4(г) начинается при г = 0 и достигает экстремума при г = 2, функция ЛГ, 4(г) начинается при г = 1 и достигает экстремума при £ = 3 и т. д. Таким образом, мы пытаемся интерполироватьу0 при £ = 2, г/, при £ = 3 и т. д.

Как показано на рис. 11.65, б, сумма

1=0

не проходит через заданные точки. Причина заключается в том, что поскольку В-сплайн функции перекрываются, различные члены этой суммы взаимодействуют таким образом, что г/(£) не достигает

Создание кривых и поверхностей

заданных точек. Для исправления этой ситуации вместо уі используется другой набор значений: с0,…, с5, так что кривая базируется уже на них, а именно:

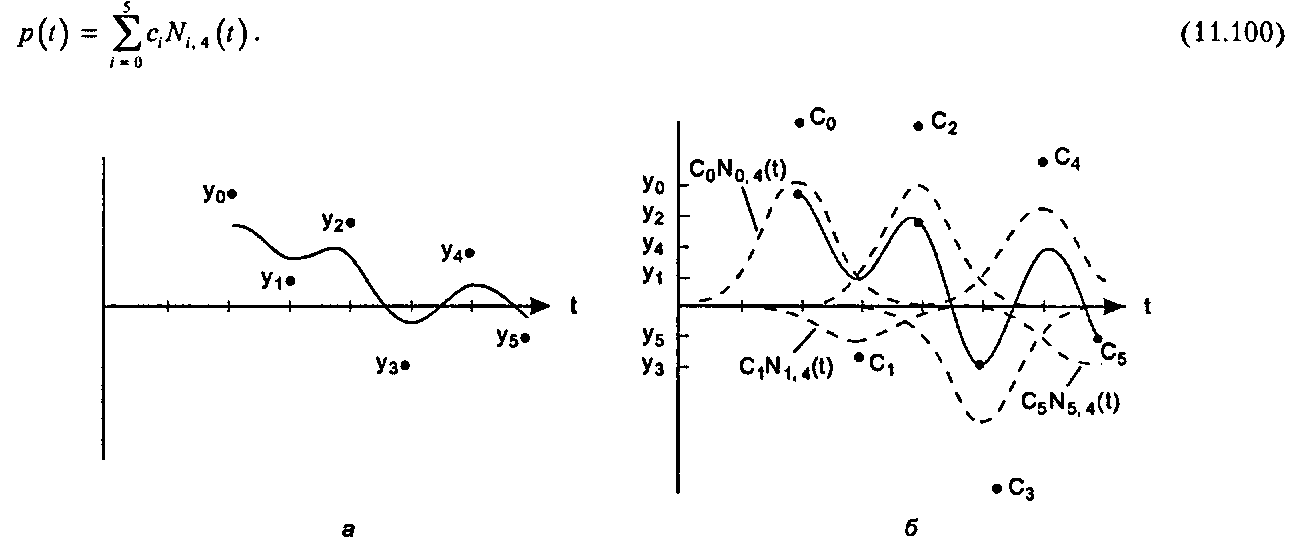
Рис 11.65. Попытка интерполяции шести точек кубическими В-сплайнами Эта кривая интерполирует все точки ур как показано на рис. 11.65, б. Мы теперь должны найти такой набор значений е., чтобы это условие действительно соблюдалось. Это может быть сделано посредством решения системы линейных уравнений. Условия интерполяции шести точек следующие"opengl1_834.html">⇐ Предыдущая| |Следующая ⇒