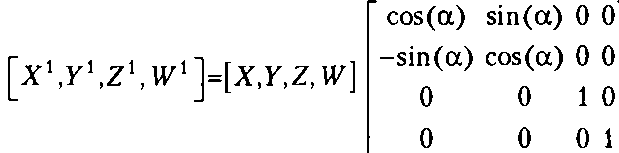
(24.5)Геометрические преобразования
координатных плоскостей, с каждой из них тоже связаны две оси. Если требуется, чтобы поворот орта оси X на 90° в положительном направлении приводил его к совмещению с направлением У, то при наблюдении из положительного направления оси Z это не всегда будет вращением против часовой стрелки. Это утверждение можно проверить на примере поворота вектора (1, 0, 0, 1) на угол 90°: г'-г-О, х{ =*со8(а)-у8И1(а)=1-0-0-1=0, у1 =х-8т(а)+у-со8(а)=1-1 + 0-0=1.
При повороте в положительном направлении на 90° вектор, направленный вдоль оси X, совместился с осью У. Но приведенное выше выражение никак не учитывает, в какой именно системе координат производится вращение. Рисунок 24.2 показывает, что если в правосторонней системе смотреть на плоскость ХУ из точки на оси 2 с положительным значением, то поворот происходит против часовой стрелки. В этом случае положительным направлением является вращение вокруг оси Z против часовой стрелки.
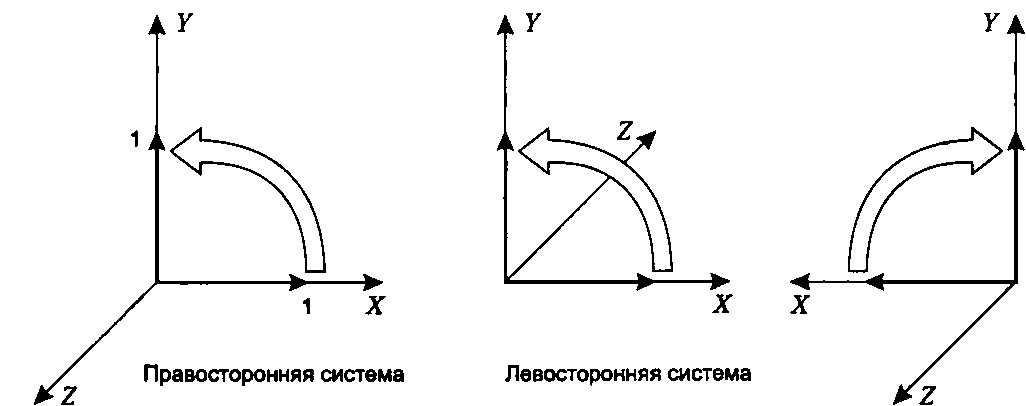
Рис. 24.2. Направление вращения при повороте на 90° Левосторонняя система на рисунке изображена дважды. В правой части рисунка она развернута осью Z к наблюдателю, чтобы показать, что в левосторонней системе та же математическая операция приведет к вращению по часовой стрелке.
Таким образом, если задавать вращение выражением (24.5) в обоих вариантах системы, будут получены противоположные положительные направления вращения. Если считать, что вращение орта оси X в положительном направлении на 90° всегда должно совмещать его с осью У, то необходимо пользоваться разными матрицами вращения в левосторонней и правосторонней системах координат.
Заметим также, что если необходимо вращать в положительном направлении не мир, а камеру, то знаки перед синусами меняются на противоположные.
Матрицы поворота точки вокруг осей X, Упри представлении вектора строкой имеют следующий вид"images/tmp6745-90.png">
(24.6).Теперь нужно повернуть на 90° в положительном направлении вокруг оси X вектор (0, 0,1), направленный вдоль оси Z:
