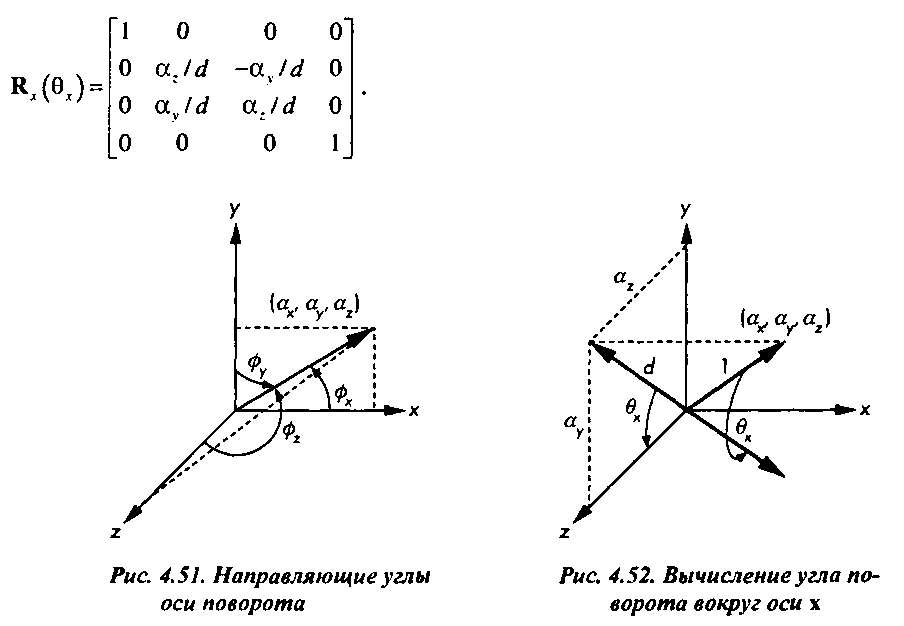
Элементы матрицы к,, вычисляются исходя из аналогичных рассуждений (рис. 4.53). Обратите внимание на то, что поворот вокруг оси у выполняется по часовой стрелке, поэтому нужно внимательно следить за знаками тех элементов матрицы, которые содержат функцию синуса. Матрица кл. будет иметь вид у
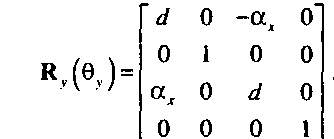
Последний шаг- перемножить матрицы отдельных преобразований: М = Т(ро) іц-Є*) іц-Є,) к.(9Г) Щву) к,(9,) Т(-ро).
Теперь рассмотрим численный пример. Пусть требуется повернуть объект на 45° вокруг прямой, которая проходит через начало координат и точку (1,2,3). Оставим фиксированную точку преобразования в начале координат. Первый шаг- оп-
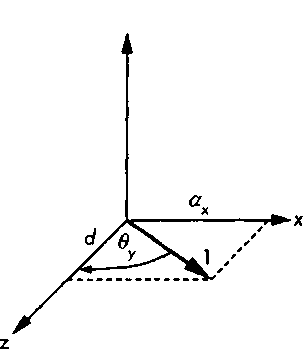
Рис 4.53. Вычисление угла поворота вокруг оси у
Объекты и геометрические преобразования
ределение точки на прямой, которая отстоит от начала координат на единичное расстояние. Эту точку получим после нормализации тройки (1, 2, 3).
Получим (\/у/\4, 2/л/Ї4, 3/>/Ї4| или в однородных координатах - (і/>/Ї4, 2/л/Ї4, 3/>/Ї4. і).
После выполнения первой фазы поворота эта точка перейдет в положение (0, 0, 1, 1). Сначала будет выполнен поворот вокруг оси х на угол, равный агссо5-Д=-. В результате точка
V13(\/у/\Л, 2і4\Л. 3/>/Ї4, і) преобразуется в точку (і/>/Ї4, 0. VIЗ/14, і), которая принадлежит
плоскости у = 0. Вокруг оси;' объект поворачивается на угол, равный агссо5л/іЗ/14 . В результате прямая окажется вытянутой вдоль оси г, и можно будет выполнить поворот вокруг этой оси на 45°. Последний этап - выполнить первые два поворота в обратном порядке и в обратном направлении. Перемножив матрицы этих преобразований, получим матрицу К"images/tmpB6CA-153.png">
Эта матрица не изменяет положение точек, которые находятся на прямой, проходящей через начало координат и точку (1,2, 3). Если потребуется выполнить такой же поворот, но фиксированная точка располагается не в начале координат, а в некоторой позиции р^, то нужно скорректировать матрицу преобразования: М = Т(ру)ИТ(-р,).
Этот пример показывает, как использовать множество простейших преобразований для выполнения сложного преобразования. Задача поворота вокруг произвольной оси и произвольной фиксированной точки возникает в множестве приложений. Варианты ее решения зависят в основном от того, каким образом задана ось поворота. Однако почти всегда можно воспользоваться описанной выше методикой для определения направляющих углов или направляющих косинусов.
