только объемы, а поверхности - это только границы объемов. Проще всего уяснить себе суть этого отличия на простом примере. Пусть необходимо смоделировать некоторый реальный объект, который имеет форму параллелепипеда. С точки зрения полигонального представления параллелепипед- это полый ящик, стенки которого сделаны из какого-либо листового материала, причем достаточно тонкого, в идеале - нулевой толщины (картон, фанера, жесть и т.п.). Этот ящик может быть закрытым (состоять из шести граней) или открытым (состоять из пяти или даже четырех граней). На экране образ открытого и закрытого ящиков будет выглядеть по-разному, если по отношению к этому образу будет применен алгоритм удаления невидимых поверхностей, но проволочное изображение закрытого ящика нельзя будет отличить от изображения открытого. В конструктивной геометрии тел ящик, как таковой, смоделировать очень трудно. В этом варианте модели примитивом является именно параллелепипед- брусок из какого-либо материала (дерева, металла, пластмассы и т.п.). Объ-
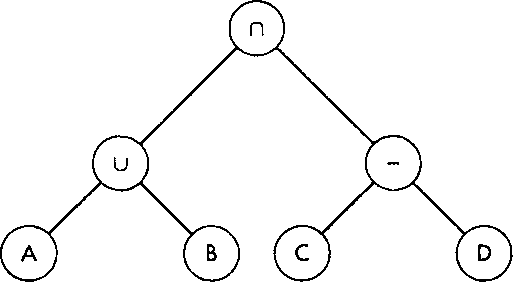
Рис. 8.23. Дерево выражения, формирующего объект методами конструктивной геометрии тел
8.9. Другие типы древовидных структур
ем бруска - основная характеристика этого объекта. Если же нам нужен именно ящик, то в конструктивной геометрии тел он создается из параллелепипедов конечной толщины, представляющих отдельные стенки (например, тарные дощечки). Нужно будет "сбить" из таких дощечек ящик точно так же, как это делает столяр. Объем ящика - сумма объемов отдельных дощечек, естественно, с учетом их толщины. При этом никто не заставляет конструктора делать ящик из дощечек одинаковой толщины - на дно можно пустить доски потолще, а боковые стенки сделать, например, из фанеры. Чтобы определить объем внутреннего пространства такого ящика, его придется чем-то "заполнить". Эта процедура выполняется с помощью все тех же базовых операций теории множеств. С подобной проблемой часто встречаются конструкторы суден. Корпус судна- это своеобразный ящик (хотя и криволинейный), а водоизмещение- это масса воды, заполняющей часть этого ящика (по ватерлинию). Конструктора интересует как объем (масса) самого корпуса, так и его водоизмещение. Решить эту задачу можно только в рамках конструктивной геометрии тел, хотя отобразить на экране форму корпуса вполне возможно и с помощью полигонального моделирования.
