Следствием из правила сложения векторов является утверждение, что для любых трех точек Р, £?, Я выполняется соотношение

(Р-<2)+(<2-/?) = (/>-/?).

Если отображать вектор Р-() в виде отрезка прямой, проведенного от точки £? к точке Р, причем для обозначения направления отрезка использовать стрелки, то правило сложения векторов может быть наглядно представлено так, как на рис. Б.6.

Геометрические объекты в аффинном пространстве обладают множеством интересных свойств. Пожалуй, наиболее важное из них состоит в том, что если использовать для представления объектов фрейм, а не систему координат, то можно единообразно представлять и векторы, и точки. Фрейм включает набор базисных векторов V,, г2,г„ и точку начала координат Р0 (точку отсчета), из которой исходят эти базисные векторы. Если в аффинном пространстве определен фрейм, то любой вектор можно представить в этом фрейме единственным образом:

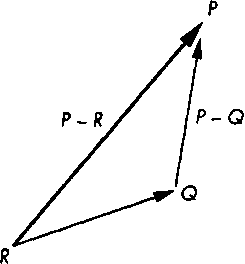
Рис. Б.6. Наглядное представление операции сложения векторов в аффинном пространстве у = а,у, +а,у, + … + а(1у„

Б.З. Аффинное пространство Любая точка также может быть единственным образом представлена в заданном фрейме"opengl5_600.html">⇐ Предыдущая| |Следующая ⇒