return (s.center - center).length () + s.radius <= radius;
}
bool intersects ( const BoundingSphere& s ) const {
return (center - s.center).lengthSq () <=
(radius + s.radius) * (radius + s.radius);
}
int classify ( const Plane& plane ) const {
float v = plane.f ( center );
if ( v > radius I I v < -radius )
return plane.classify ( center ) ;
return IN_BOTH;
}
};Еще одним часто встречающимся примером ограничивающего тела является прямоугольный параллелепипед с ребрами, параллельными осям координат {axis-aligned bounding box - ААВВ). Простейшим способом задания такого тела является задание двух точек р^п и р11ах, представляющих
собой покоординатные значения минимума и максимума из координат, содержащихся внутри точек.
Тогда, если задан набор точек у0, v,упл , то Рш..=т[п »,..<< Л*,™,,, (37) ^ах., =тах^..
Проверка на попадание точки р внутрь такого офаничивающего тела сводится к проверке выполнения следующих неравенств: Рпйп.х ~ Рх ~ Ртлх.х'
Рпт.у ~ Ру - Ртах.., ' (3-8) Ртлп,2 ~ Рг ~ Ртах^'
Аналогично при помощи покомпонентных неравенств выполняется проверка на пересечение двух ААВВ или попадание одного ААВВ внутрь другого.
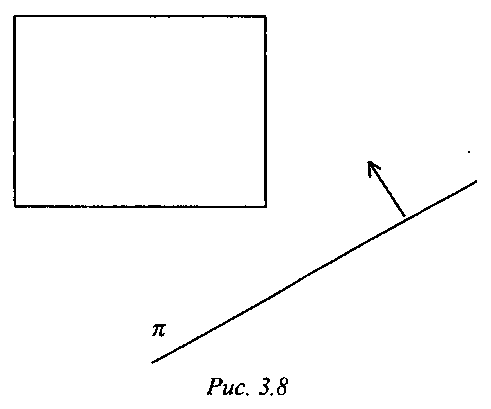
Рассмотрим теперь, каким образом осуществляется классификация ААВВ относительно плоскости я: (и, + ^ =0 (рис. 3.8).
Если вектор п единичный, то для произвольной точки р величина /(р) = (п,р) + с1 по модулю
равна расстоянию отэтой точки до плоскости. Знак этой величины будет положительным, если точка лежит в положительном полупространстве ((р, л) + й?>0) и отрицательна в противном случае. Эту величину обычно называют расстоянием до плоскости со знаком.
Самым простым способом будет вычисление значения /(р) = (п, р) + о!
для всех восьми вершин ААВВ. Если все эти значения имеют одинаковый знак, то параллелепипед целиком лежит в соответствующем полупространстве. Однако этот процесс можно оптимизировать.
Простейшие геометрические алгоритмы и структуры
Обычно часто возникает необходимость сравнения целого набора ограничивающих тел с заданной плоскостью к. В этом случае вместо вычисления значения / во всех вершинах параллелепипеда достаточно вычислить >то значение всего в одной вершине, индекс которой определяется ориентацией вектора нормали к плоскости. На рис. 3.9, а-г показаны различные варианты расположения плоскости по отношению к ограничивающему телу и выделена соответствующая вершина для каждого из случаев.
