Для начала определим коэффициенты плоскости п2: (и2, р)+d2 = 0.
"2 =[vi-vo^v2-vq]' d2=-(n2,vQ). (3.17) Далее находятся расстояния со знаком ото всех вершин треугольника 7, до плоскости л2 (с точностью до постоянного множителя ||и21|2) путем подстановки вершин в уравнение плоскости.
<=("2."() + rf2- (318)Если они все имеют одинаковый знак и отличны от нуля, то 7j целиком лежит по одну сторону щ и пересечения нет.
То же самое проделывается для Г2 и л,. Это позволяет сразу же отбросить целый ряд часто встречающихся случаев.
Если все du = 0, то треугольники Тх и Г2 лежат в одной плоскости, этот
случай будет рассмотрен чуть позже.
В противном случае находим пересечение плоскостей л, и л2. Это будет прямая, задаваемая уравнением / = org +1 dir, где dir = [и,, п2 ] направляющий вектор этой прямой. Заметим, что оба треугольника пересекают эту прямую (в противном случае они были бы отброшены раньше) и в результате каждого пересечения получается отрезок на этой прямой. Эти отрезки пересекаются между собой тогда и только тогда, когда пересекаются исходные треугольники.
Простейшие геометрические алгоритмы и структуры
Рассмотрим, каким образом находится пересечение треугольника Tj и прямой (второе пересечение находится аналогично).
Первым шагом будет проектирование вершин и0, и,, и2 на прямую
рщ = (dir,ui -org). (3.19)
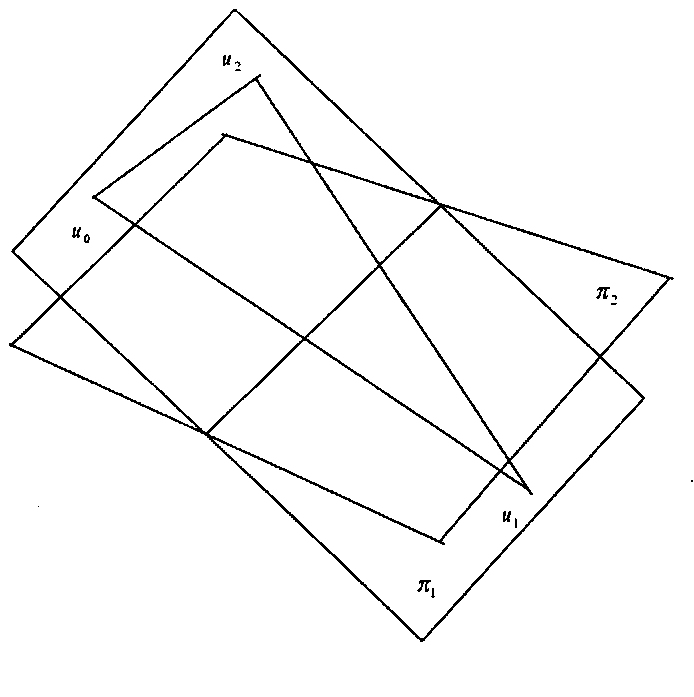
Далее мы будем считать, что вершины и0,и2 лежат по одну сторону от л2, а и, - по другую (рис. 3.17).
Рис. 3.17
Найдем пересечение ребра и0и, с прямой / = org +1 dir. Для этого достаточно найти значение параметра t, соответствующее точке пересечения.
Отрезок и0и1 можно представить в параметрической форме как Р = и0 + ос(и, -и„), осе [0,1] Тогда уравнение для точки пересечения ребра п прямой может быть записано как и0+а(и,-и0) = org +tdir. (3.20)
Умножим это уравнение скалярно на я2. Так как точка пересечения лежит на обеих плоскостях, то (org +t dir, п,) + аг = 0. Отсюда получаем уравнение для параметра а :
