Аналитическое исследование неполнодоступных систем при обслуживании вызовов с ожиданием достаточно сложно из-за значительного числа состояний системы обслуживания. Известны работы [7.1, 7.7], где иссле дованы идеально симметричные системы с ограниченным числом мест ожидания и неограниченным временем ожидания.

Ниже рассмотрена идеально симметричная система с ограниченным ожиданием (конечная очередь, ограниченное время ожидания) [7.5]. Для этой системы рассчитаны вероятностные характеристики (вероятности стационарного состояния, вероятность потерь по вызовам).

7.2.1. Описание модели На К-линейную идеально симметричную систему доступности с/ поступает простейший поток вызовов интенсивности X. Поступивший вызов занимает доступный выход на случайное время, распределенное по показательному закону с параметром ц.

Если в момент поступления вызова имеется хотя бы один свободный доступный выход, вызов начинает обслуживаться. Если в момент поступления вызова свободные выходы отсутствуют, то вызов ставится в очередь на ожидание обслуживания при наличии хотя бы одного свободного из Я мест ожидания. Освободившийся выход немедленно занимается первым выбранным в порядке поступления ждущим вызовом, которому доступен данный выход. Если за время а ждущий вызов не начал обслуживаться, он будет потерян.

Для идеально симметричной схемы известно выражение условной вероятности потерь:

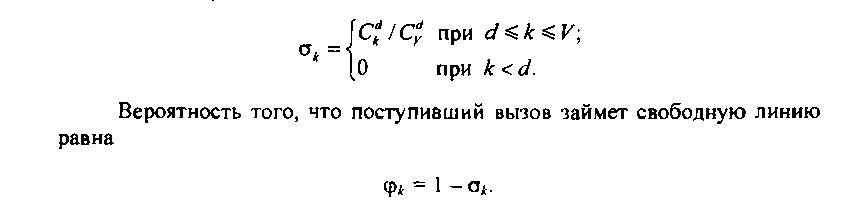
При рассмотрении системы с ожиданием необходимо получить условную вероятность того, что ждущий вызов не сможет занять освободившийся выход из к занятых выходов. Очевидно, для ждущего вызова все <1 доступных этому вызову выходов находятся в числе к занятых, следовательно, вероятность занятия данным ждущим вызовом освободившейся ли _сс! с1

нии 5* =- и, соответственно, q_k=1--.

к к Из вероятностных соображений несложно доказать, что для неполнодоступного включения произвольного вида будет выполняться соотношение

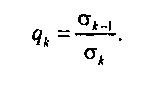
Для вероятностного описания системы введем случайный процесс Л(0⁼(КО. 9(0. £i(0> •••> £е«(0)> который содержит дискретные компоненты: v(t) - число занятых выходов в момент t; 0(0 - число занятых мест ожидания в момент t и вектор дополнительных координат й,(0, £г(0. •••. 0» 4в(о(0)>^гД^е- время пребывания в системе заявки, занимающей в очереди j-e место. Процесс п(0 относится к классу конечномерных кусочнолинейных марковских процессов [7.2]. Важной особенностью этого процесса является упорядоченность вектора дополнительных координат 0), где £,{/) - время пребывания в системе заявки, занимающей в очереди j-e место.

Процесс т](0 относится к классу конечно-мерных кусочно-линейных марковских процессов [7.2]. Его важной особенностью т](0 является упорядоченность вектора дополнительных координат

Р{а > 4,(0 > Ш > … > Ш >0} = 1.

Введем обозначение

Pu(t, х_и…, х,) = />{v(0 = к, 0(0 = I, xj-h < ^/t) < xj, j = 1,1}.

Так как событие v(/) = к. 0(0 = /. х,- h < bjf) < x_hj = 1,1} при 0 < x_t< < … < хг < x\ < а содержится в событии (в интервалах времени (/ - xj- h, t - Xj),j = 1…/ в систему поступили заявки), то справедливо неравенство: Л./(Л *...... х{) < (Xh)'.

Полученное неравенство означает, что рассматриваемые вероятности абсолютно непрерывны в 1-мерных областях = (0 < X, < … < х, $ а). Таким образом доказано существование плотностей fit, к, I, х\,…, xj) у распределения Pkjit, х\,…, xi). При этом

f(t, к, /, х_и…, xj)h' = P{v(t) = к, 0(0 = I xj-h < %,{i)Xj, j = \,l}.

Рассмотрев возможные переходы между состояниями идеальной симметричной неполнодоступной системы с ограниченным ожиданием, перейдем к составлению уравнений равновесия рассматриваемого случайного процесса.

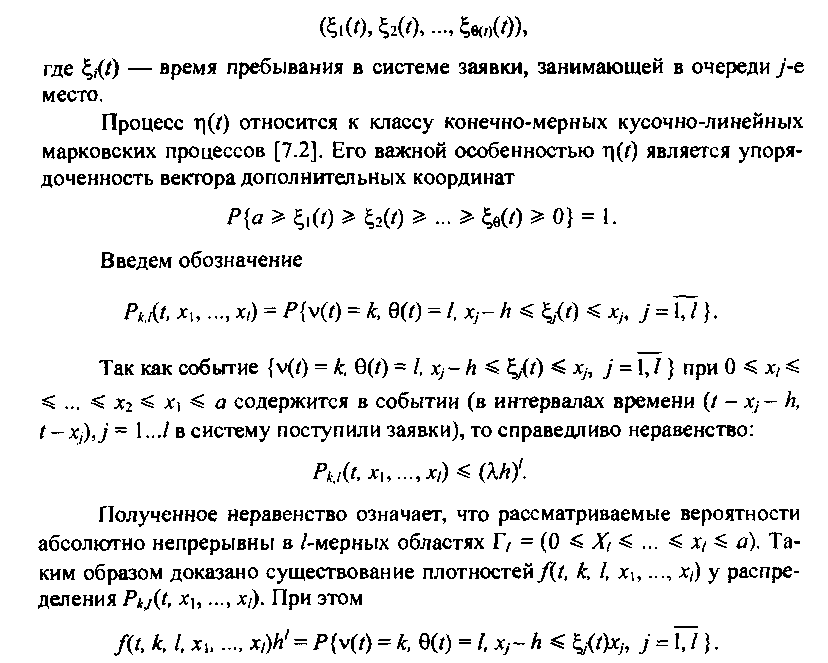
Исследуем графы состояний описаний модели (рис. 7.5, 7.6). Для единообразия записи переходных вероятностей и уравнений введем

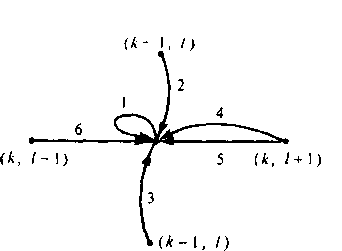
Рис. 7.5. Граф состояний идеально симметричной системы при / = 1, Л -1, к -Ы,У

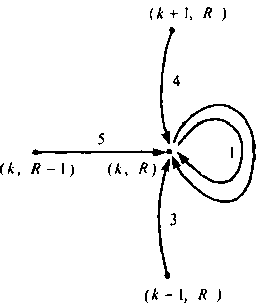
Рис. 7.6. Г раф состояний идеально симметричной системы при к=с1,У

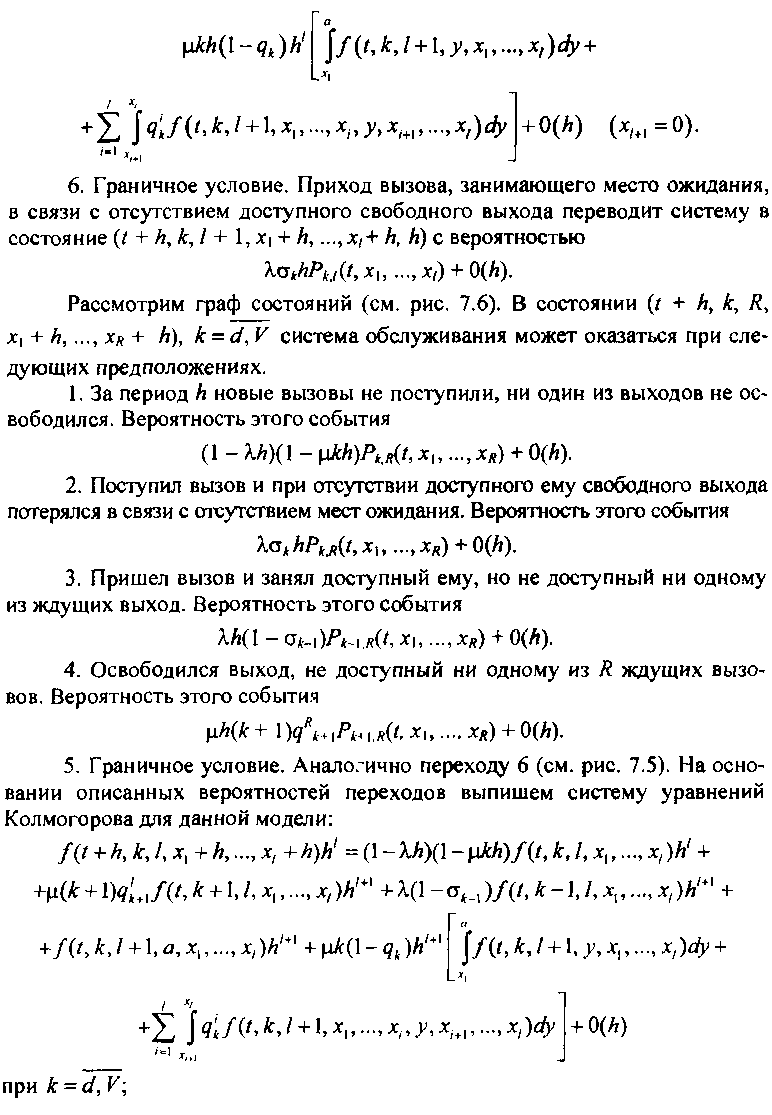
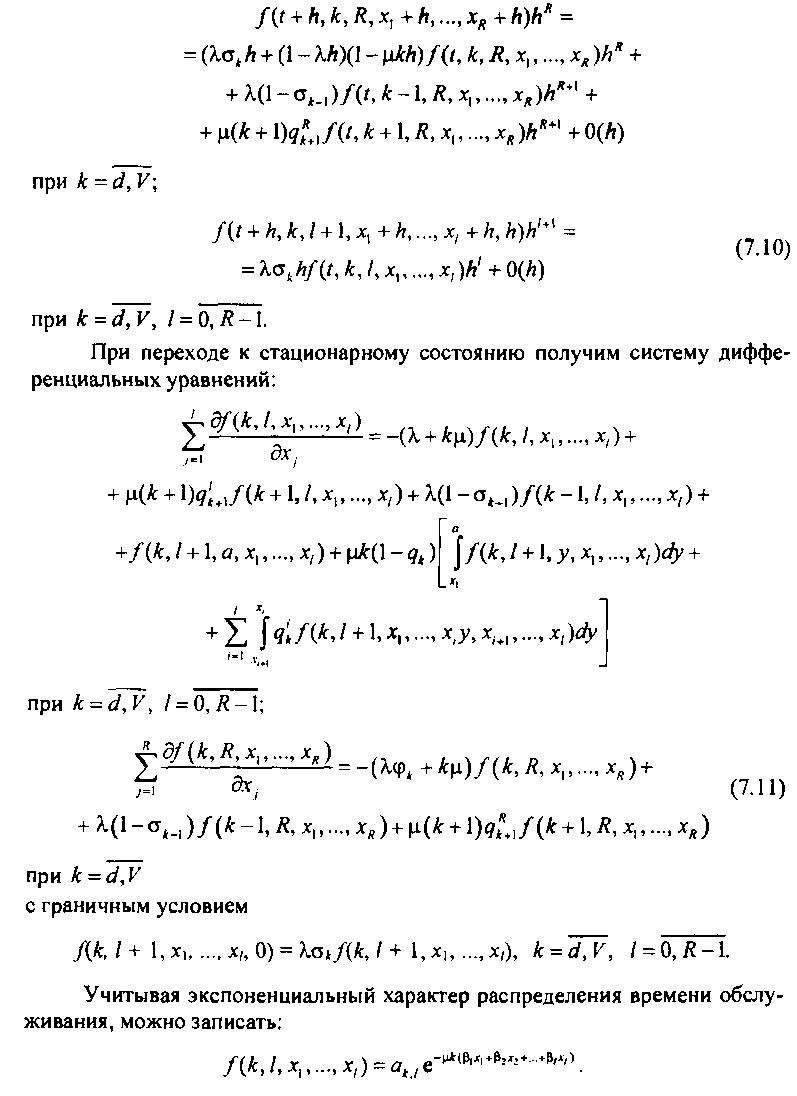
Коэффициент Р/ представляет собой вероятность, с которой заявка, стоящая в очереди на 1-м месте, может быть принята на обслуживание при освобождении ОДНОГО ИЗ ВЫХОДОВ системы В интервале (/-*1, 0.

Для

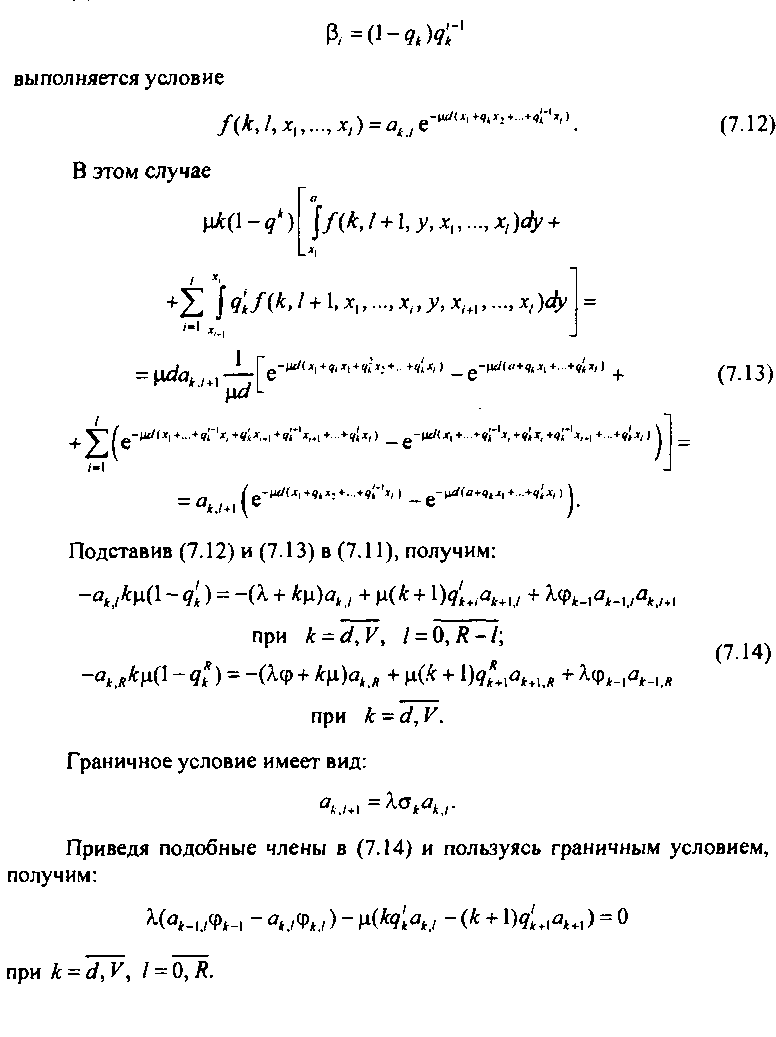
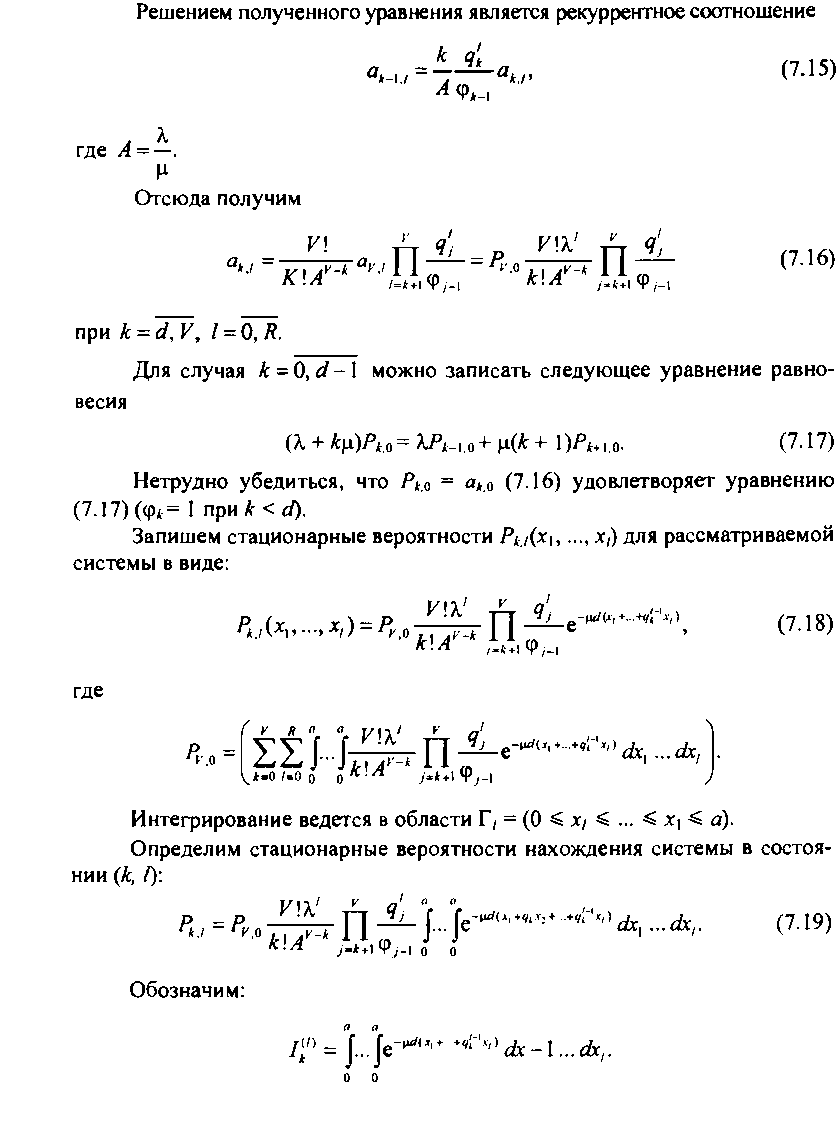
Тогда последовательным интегрированием по области Г, получим:

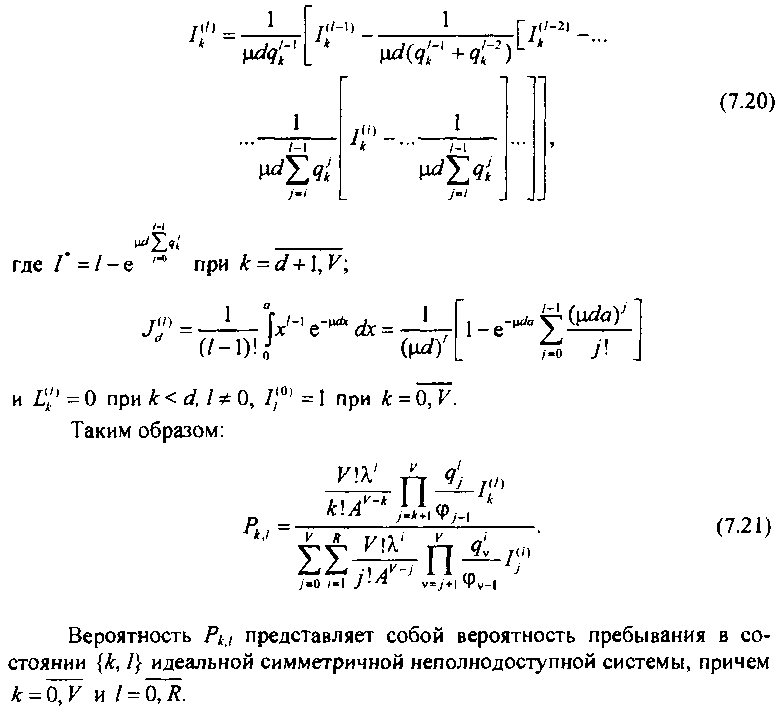
7.2.3. Вероятность потерь по вызовам Вызов, поступивший в систему, получит отказ в обслуживании в случае занятости всех доступных выходов и всех мест ожидания. Кроме того, ожидающий вызов, не обслуженный в течение времени а, также будет потерян. Вероятность потерь по вызовам равна сумме вероятностей указанных выше событий (несовместных). Вероятность занятости всех доступных выходов и всех мест ожидания имеет вид:

Для вывода выражения вероятности потерь Р (потери за счет превышения ждущими вызовами допустимого времени ожидания) введем в рассмотрение следующие события:

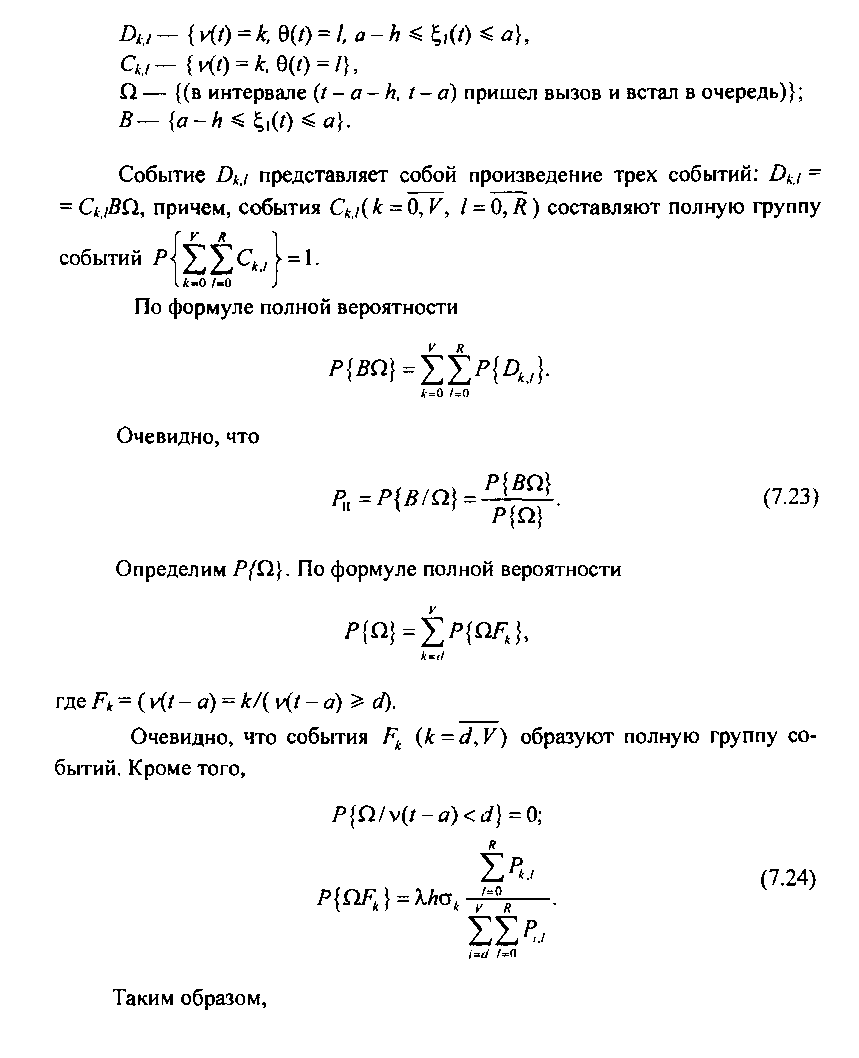
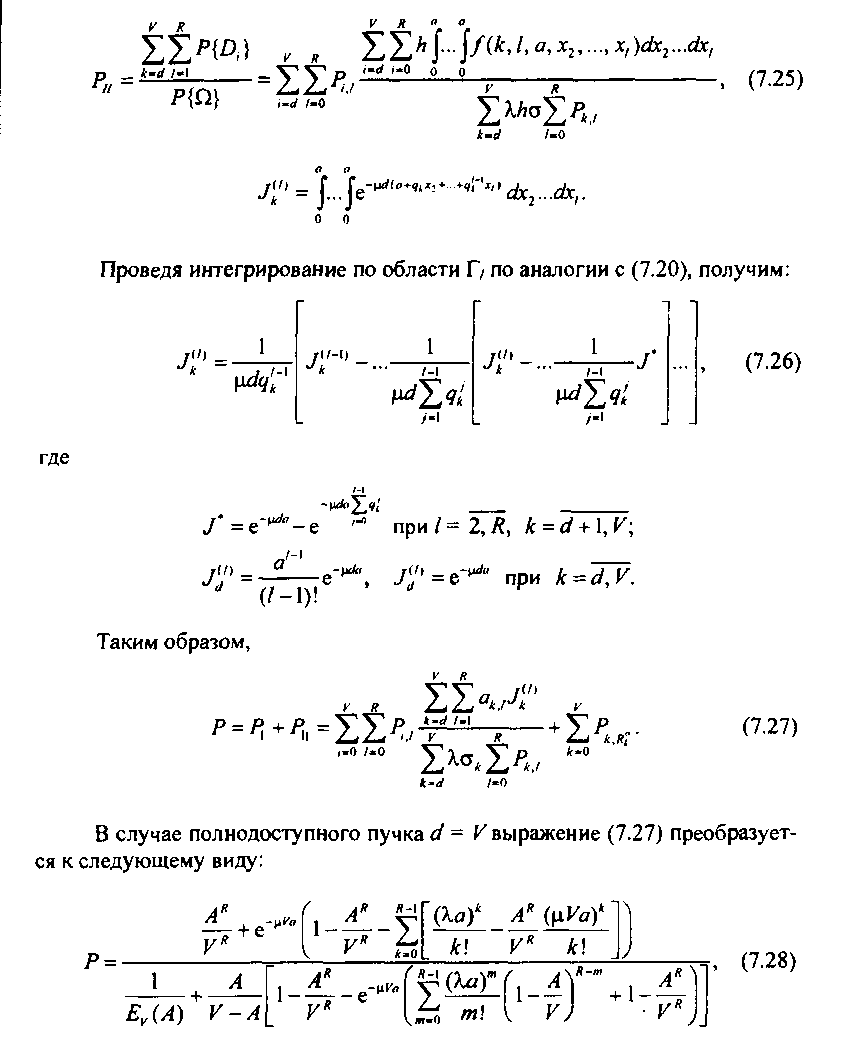
где £р(Л) - вероятность потерь в системе с явными потерями.

Учитывая сложность полученных выше выражений, приведем алгоритм расчета рассматриваемой системы на ЭВМ.

На основании выражений (7.15) и (7.16), приняв Р_к0= 1, рекуррентно рассчитываем коэффициенты а :

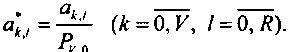
На основании выражения (7.20) рекуррентно рассчитываем таблицу интегралов/*^(/)(к = с!,У, I = 1, Л).

По выражению (7.18) получим значение /V,о

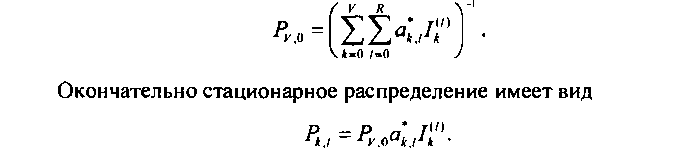
На основании выражения (7.26) рекуррентно рассчитываем таблицу интегралов (к = d,V,1 = 1, /? )■ Воспользовавшись выражением (7.27), рассчитываем вероятность потерь по вызовам.

В заключение этого раздела необходимо отметить, что для идеально симметричной неполнодоступной системы с конечной очередью, ограниченным временем ожидания, пуассоновским входным потоком и экспоненциальным обслуживанием получено стационарное распределение числа заявок в системе, а также выражение для расчета вероятности потерь по вызовам и разработан вычислительный алгоритм; полученные результаты могут быть использованы для приближенного расчета различных неполнодоступных систем, обслуживающих приборов узла коммутации ЦСИС, а также оценки вероятностных характеристик многозвенных коммутационных систем, работающих с ограниченным ожиданием.

Литература 7.1. Арутюнян A.B. Изучение идеально симметричных схем с потерями, ожиданием и уходом из очереди // Информационные сети и их структура. М.: Наука, 1976.

7.2. Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. М.: Наука, 1987.

7.3. Денисьева О.М. Системы массового обслуживания с ограниченным ожиданием. М.: Радио и связь, 1986.

7.4. Ершов В.А., Пупко М.А. Расчет вероятности потерь по вызовам в многоканальной СМО с входным потоком, зависящим от состояния системы, конечной очередью и конечным временем ожидания // Сборник научных трудов ЦНИИС. «Системы коммутации с программным управлением». М.: ЦНИИС, 1989. С. 70-78.

7.5. Ершов В.А., Пупко М.А. Идеально симметричная неполнодоступная система с ограниченным временем ожидания и конечной очередью // Сборник научных трудов ЦНИИС. «Системы коммутации с программным управлением». М.: ЦНИИС, 1989. С. 50-61.

7.6. Поляев Л.Н. Аналитические методы анализа систем массового обслуживания с ограничениями. Канд. дисс. М., 1984.

7.7. Седол Я.Я. Определение вероятностных характеристик неполнодоступной схемы с потерями и ожиданием // Проблемы определения информации. М.: Наука, 1973.

7.8. Теория телетрафика. Штермер X., Белендорф Э., Бининда Н. и др. / Под ред. Г.П. Башарина. М.: Связь, 1971.

Расчеты, значения которых кажутся всем несущественными, всегда бывают источником наибольших ошибок.

Закон Морфи

⇐Полнодоступный пучок обслуживающих приборов с ограниченным ожиданием и конечной очередью | Мультисервисные телекоммуникационные сети | Постановка задачи⇒