glEnd:Второй способ более эффективен, так как позволяет избежать непроизводительных издержек, связанных с многократными вызовами gl Begin и gl End.
Рис. 2.25. Множество из 500 случайных точек На рис. 2.25 показан типичный график, который может получиться в результате такого построения. Только «однородная» плотность точек на всем пространстве квадрата сможет убедить вас в том, что величины в диапазоне 0 … Ы- 1 появляются примерно с одинаковой вероятностью и что не существует видимой зависимости между одной величиной и другой, следующей за ней.
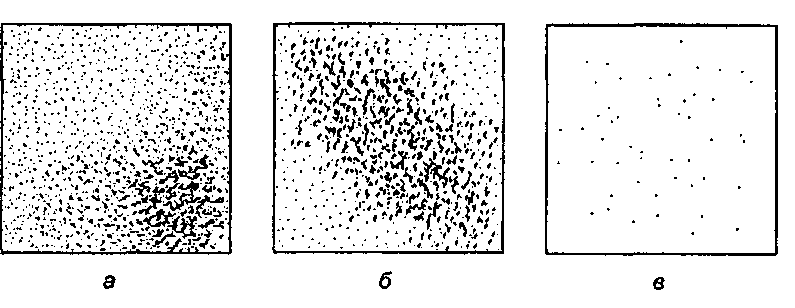
Рис. 2.26. Графики рассеяния, построенные плохими генераторами случайных чисел Рисунок 2.26 показывает, что может произойти, если ГСЧ плохой. На графике а) наблюдается слишком высокая плотность некоторых величин, так что распределение в промежутке 0… ЛГ- 1 неодинаково. В случае 6) имеет место сильная корреляция между соседними числами последовательности. Когда одно из чисел велико, то следующее имеет тенденцию быть маленьким. Наконец, случай в) показывает, вероятно, худшую ситуацию из всех"images/tmp8E4A-70.png">
Начальная стадия: рисование фигур
Рисование подобных совокупностей точек дает возможность грубой проверки генерируемых чисел на равномерность. Этот тест, однако, далек от совершенства [Кнут, 123].
Напишите программу для создания графиков случайных точек, используя несколько различных ГСЧ для формирования пар (х, у). Испробуйте различные константы А, В и ЛГв основном ГСЧ и оцените, как это повлияет на совокупности точек. Внимание] Если созвездие точек внезапно «застыло» и не появляется никаких новых точек, это может означать, что комбинация чисел просто повторяется.
Тематическое задание 2.2. Введение в систему итерируемых функций Из его рая нас никто не изгонит. Дэвид Гильберт (David Hilbert), защищающий теорию множеств Кантора Уровень сложности И.
Повторяющаяся операция рисования ковра Серпинского является одним из примеров системы итерируемых функций (iterated function system - IFS), с которой мы будем сталкиваться на протяжении всей этой книги удивительно часто. Многие интересные компьютерные рисунки (фракталы, множество Мандельброта и т. д.) построены на вариантах этой IFS.
