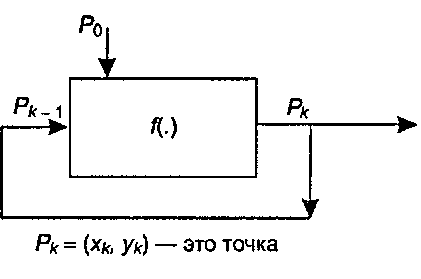
Рис. 2.28. Генератор последовательности итерируемых функций для точек Отступление. Взгляд на ковер Серпинского как как IFS

В терминологии IFS k-я точка ковра Серпинского, рк, получается из предыдущей точки pkl по следующей формуле"opengl1_132.html">⇐ Предыдущая| |Следующая ⇒