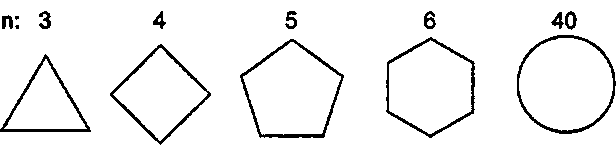
Рис. 3.30. Примеры п-угольников Вершины я-угольника лежат на так называемой порождающей окружности (parent circle) данного и-угольника, и их расположение легко вычисляется. Случай шестиугольника (гексагона) показан на рис. 3.31; его вершины расположены на одинаковом расстоянии через каждые 60° по окружности. Центр порождающей окружности радиуса R (на рисунке она не показана) находится в начале координат, а первая вершина Р0 лежит на положительной части оси х. Другие вершины располагаются следующим образом"images/tmp8E4A-114.png" alt="Нахождение вершин 6-угольника">

Рис 3.31. Нахождение вершин 6-угольника Листинг 3.12. Построение п-угольника в памяти

void ngon(int п. float ex. float су. float radius, float rotAngle) {

// assumes global Canvas object, cvs

// принимает глобальный объект класса Canvas - cvs

if(n < 3) return; // bad number of sides // недопустимое число сторон

double angle - rotAngle * 3.14159265 / 180; // initial angle // начальный угол

double anglelnc - 2 * 3.14159265 /n; // angle increment // увеличение угла

cvs.moveToCradius * cos(angle) + ex.radius * sin(angle) + cy);

for(int k - 0"opengl1_178.html">⇐ Предыдущая| |Следующая ⇒