}
}Пример 3.6.1. Рисование п-угольника с помощью черепахи Столь же просто рисовать и-угольник с использованием черепашьей графики. На рис. 3.32 показано, как рисовать правильный шестиугольник. Начальные позиция и направление отмечены маленьким треугольником. Черепаха просто движется вперед (forward) шесть раз, делая CCW-поворот (то есть против часовой стрелки) на 60° после каждого перемещения. Соответствующий код выглядит так:
for (i = 0; i < 6: i++) {
cvs.forward(L. 1): cvs.tum(60);
}Одна вершина расположена в начальной CP, причем как CP, так и CD остаются неизменными на протяжении всего процесса. Рисование п-угольника общего вида, а также некоторых его вариантов, рассматриваются в упражнениях.
3.6. Фигуры на основе правильных многоугольников
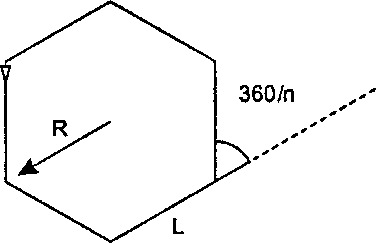
Рис. 3.32. Рисование 6-угольника
3.6.2. Вариации п-утольников На базе вершин я-угольника можно нарисовать также интересные вариации. Эти вершины можно соединять различными способами, в результате чего образуется целый ряд фигур, как показано на рис. 3.33. На рис. 3.33, а нарисован стандартный я-угольник"images/tmp8E4A-116.png">
а б в Рис. 3.33. Правильный семиугольник и его потомки: а) 7-угольник; б) звездчатая форма; в) 7-розетка Пример 3.6.2. Розетка и золотая 5-розетка Розеткой называется я-угольник, у которого каждая вершина соединена со всеми остальными вершинами. На рис. 3.34 показаны 5-, 11- и 17-розетки. Иногда розетку используют в качестве тестового узора для устройств компьютерной графики. Ее правильная форма сразу показывает любые искажения, а разрешающую способность тестируемого устройства можно определить, фиксируя количество «уплотнений» (crowding) и размытий (blurring), демонстрируемых пучками линий, сходящихся в каждой вершине.
