Пример 3.7.1. Плавное сопряжение дуг Используя две касающиеся друг друга окружности, мы можем получить более сложные формы. Рисунок 3.41 иллюстрирует основной принцип. Две окружности касаются друг друга в точке А и имеют в ней общую касательную Ь. В силу этого две дуги, выделенные жирной линией, плавно сопрягаются друг с другом, и в точке А не видно никакого шва, разрыва или излома. Подобным же образом дуга окружности может быть плавно сопряжена с произвольной касательной, как это видно в точке В.
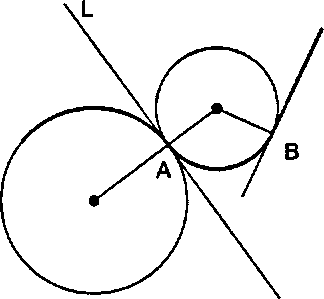
Рис. 3.44. Плавное сопряжение дуг с помощью касающихся окружностей Практические упражнения 3.7.1. Философский смысл кругов В китайской философии и религии два принципа - инь и янь - взаимодействуют, влияя на судьбу всех живых существ. На рис. 3.45 показан изысканный символ инь-янь. Его темная часть - инь - символизирует женское начало, а светлая часть - янь - мужское. Подробно опишите геометрию этого символа, предположив, что он находится в начале некоторой системы координат.

Рис. 3.45. Символ инь-янь
3.7.2. Семь монет
Опишите конфигурацию на рис. 3.46, где шесть монет компактно размещены вокруг седьмой, центральной. Исходя из соображений симметрии, объясните причину этой компактности - почему каждая внешняя монета в точности касается своих трех соседей.
3.7.3. Знаменитый логотип На рис. 3.47 изображен знаменитый автомобильный логотип, созданный путем помещения треугольников внутрь равностороннего треугольника, причем вокруг внешнего (не показанного) треугольника
6 Ф. Хилл
Дополнительные инструменты для рисования
описаны две концентрические окружности. Определив «правильное» расположение трех внутренних точек, напишите подпрограмму для рисования этого логотипа.
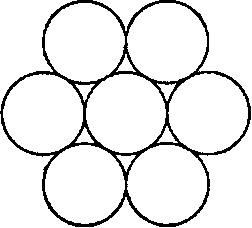

Рис. 3.46. Семь окружностей Рис. 3.47. Знаменитый логотип
3.7.4. Рисование часов и подобных им фигур
Окружности и прямые можно заставить касаться друг друга различными способами, чтобы получились симпатичные гладкие кривые, как на рис. 3.48, а. На рис. 3.48, б показаны основные прямые и окружности. Напишите подпрограмму, рисующую такую форму, специфическую для часов.
