Еще один классический пример - эллипс, небольшое обобщение круга. Параметрически эллипс описывается следующим образом:
x(t) = Wcos(t),
y(t)-Hsia(t)juui0utu2n. (313)1 Etch-a-Sketch является торговой маркой фирмы Ohio Art.
Дополнительные инструменты для рисования
где V/-.«полуширина» (большая полуось), а Я- «полувысота» (малая полуось) эллипса. Некоторые геометрические свойства эллипса исследуются в упражнениях. Если "/равно Я, то эллипс превращается в круг радиуса \У. На рис. 3.55 показан эллипс, а также координатные функции х(.) и г/(.).
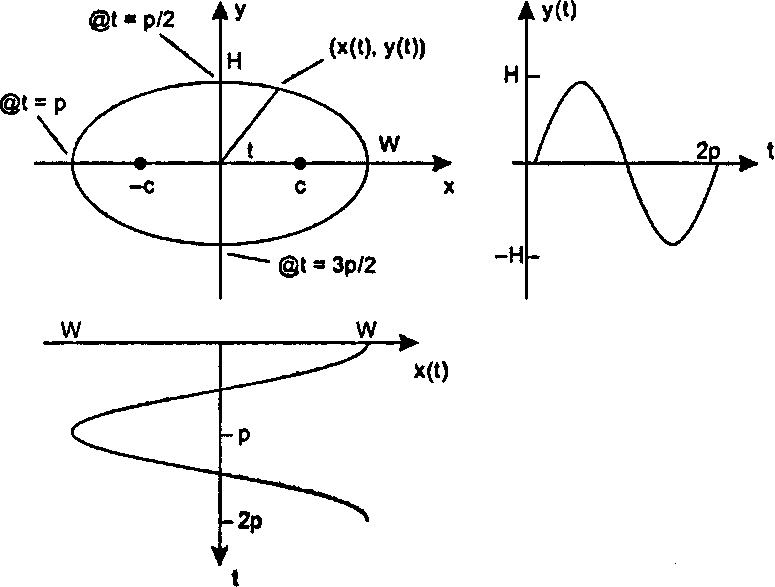
Рис. 3.55. Эллипс, заданный параметрически Когда t изменяется от 0 до 2я, точка P(t) - (x(f), y(t)) обходит эллипс один раз, начиная (и заканчивая) свое движение в точке ( W, 0). На рисунке показано, где находится эта точка при различных значениях t. Полезно наглядно представить процесс рисования эллипса на «Волшебном экране». Нужно волнообразно поворачивать рукоятки взад и вперед, чтобы одна из этих рукояток имитировала cos(f), а вторая - sin(£). (Это удивительно трудно проделать вручную.)
Преобразование параметрической формы в неявную
Предположим, мы хотим убедиться в том, что параметрическая форма из уравнения (3.13) действительно представляет эллипс. Как мы сможем извлечь неявную форму из параметрической? Первый шаг состоит в объединении двух уравнений для x(t) и у(£), чтобы каким-то образом исключить переменную t. Результатом этою преобразования будет соотношение, которое должно выполняться для ecext. Не всегда очевидно, как сделать это, поскольку не существует простых правил, применимых для всех параметрических форм. В случае эллипса, например, мы можем возвести в квадрат оба отношения x/Wи у/Ни использовать известное тождество cos(f)2 + sin(f)2= 1, чтобы в результате получить знакомое уравнение эллипса"images/tmp8E4A-141.png">
(3.14)В последующих упражнениях исследуются свойства эллипса и других «классических кривых». В них даются полезные сведения о конических сечениях (conic sections) - сведения, которые будут использованы позднее. Прочтите упражнения до конца, даже если вы не собираетесь решать каждое из них.
