Замеры P(t) предварительно записываются в соответствующий массив Р[1], i = 0 .1.....п. Ломаная линия рисуется путем прохождения последовательности значений i каким-либо интересным путем. Это означает, что последовательность г0, i,,… компонуется из значений от 0 до п, причем для каждого индекса ik осуществляется вызов функции worldL1neTo(P[ik]). Возможны следующие варианты: О «Случайная раздача»: последовательность i0, i,,… представляет собой случайную перестановку величин 0, 1,п, аналогично раздаче заданного количества карт из перетасованной колоды.
О Каждая пара точек соединяется прямой линией. Поэтому каждая пара значений в диапазоне О, 1.....п появляется на соседних местах где-нибудь в последовательности i0, i,.....Одним из примеров того, как рисуются линии посредством соединения каждой точки со всеми остальными, является простая розетка.
3.10. Тематические задания О Можно также рисовать «паутины», как предлагается на рис. 3.78. Здесь индекс многократно циклически принимает все возможные значения, пропуская каждый раз некоторое число М. Это может быть легко сделано, если последующий индекс формировать из предыдущего по формуле г = (I + М) тод(п + 1).
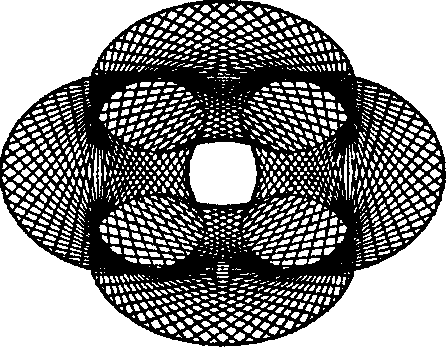
Рис. 3.78. Добавление «паутин» к кривой Тематическое задание 3.8. Окружности, вращающиеся вокруг окружностей Уровень сложности II.
Еще одно большое семейство интересных кривых, которые могут быть использованы в графике. Рассмотрим путь, который проходит точка, жестко закрепленная на окружности, в то время как эта окружность вращается вокруг другой зафиксированной окружности. Кривые, являющиеся траекториями таких точек, называются трохоидами (trochoids), и на рис. 3.79 показано, как они образуются. Точка, предназначенная для трассировки, прикрепляется к вращающейся окружности (радиуса Ь) на конец стержня на расстоянии k единиц от центра окружности. Радиус зафиксированной окружности составляет а единиц. Существует два основных вида трохоид"opengl1_213.html">⇐ Предыдущая| |Следующая ⇒
