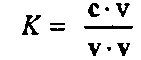
Аналогично скалярно умножим обе части уравнения (4.22) на вектор Vі и получим: м =
С V
V-Vпричем мы использовали третье свойство из равенств (4.21). Собирая все воедино, имеем:
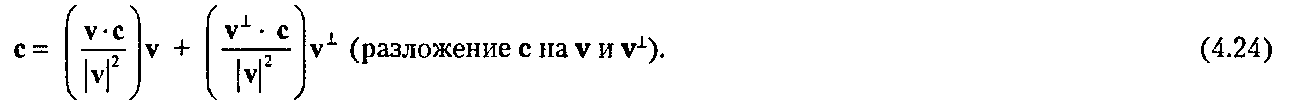
Данное равенство применимо для любых векторов с и v. Та часть вектора, которая направлена вдоль v, носит название ортогональной проекции (orthogonal projection) вектора с на вектор v. Второй член в явном и компактном виде представляет «разностный член»; его модуль равен расстоянию от точки С до прямой:
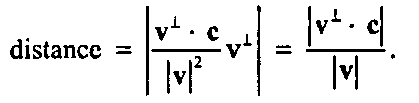
(Убедитесь сами, что второе выражение действительно равно первому.) Возвращаясь к рис. 4.13, б, мы можем сказать, что расстояние от точки С до прямой, проходящей через точку Л в направлении у, равно:

Пример 4.3.5
Найдите ортогональную проекцию вектора с = (6,4) на вектор а = (1, 2). (Нарисуйте соответствующие векторы.) Решение Вычислите первый член равенства (4.24) и получите вектор (14,28)/5. Пример 4.3.6
На каком расстоянии находится точка С = (6,4) от прямой, проходящей через точки (1,1) и (4,9)?
Векторные инструменты для графики
Решение Задайте точку Л = (1,1), возьмите вектор v = (4,9) - (1,1) = (3,8) и вычислите distance (расстояние) по формуле (4.25): результат должен быть таким: distance = 31/V73.
Практические упражнения
4.3.10. Разложение Представьте вектор g = (4,7) в виде линейной комбинации векторов b = (3,5) и Ь1. На каком расстоянии находится вектор (4,2) + g от прямой, проходящей через точку (4,2) в направлении вектора Ь?
4.3.11. Блок, спускаемый по наклонной плоскости Блок покоится на наклонной плоскости, наклоненной под 30° относительно горизонтали. На блок действует сила тяжести величиной в один ньютон. Какова величина составляющей силы тяжести, движущей этот блок вдоль наклонной плоскости?
4.3.12. Расстояние от прямой до точки На каком расстоянии от прямой, проходящей через точки (2,5) и (4, -1), расположена точка (6,11)? Проверьте полученный результат на миллиметровке.
4.3.6. Приложения проекции: отражения Для того чтобы отобразить на дисплее отражение света от зеркала или поведение соударяющихся бильярдных шаров, нам необходимо найти то направление, которое получает объект после отражения от заданной поверхности. В тематическом задании, находящемся в конце данной главы, описывается приложение, которое прослеживает путь луча света, когда тот отражается от различных точек внутренней поверхности комнаты, или путь бильярдного шара при его отскакивании от бортов стола. Как будет показано в данном разделе, при каждом отражении луч света или бильярдный шар движутся в новом направлении.
