Известно, что когда луч света отражается от зеркала, угол отражения должен равняться углу падения. Позднее мы покажем, как использовать векторы и проекции для вычисления направления, в котором отражается свет. Для простоты мы можем рассуждать в терминах двумерных векторов, но поскольку при выводе размерности векторов не фигурируют явно, полученный результат будет верен и для случая трех измерений при отражении от поверхности.

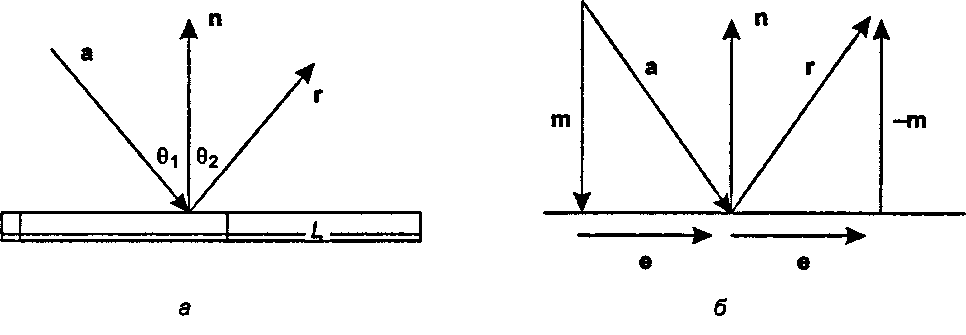
Рис. 4.14. Отражение луча от поверхности Луч, изображенный на рис. 4.14 а, движется в направлении а, попадает на прямую Ь и отражается в направлении г, которое пока неизвестно. Вектор п перпендикулярен прямой. Угол 0( должен быть равен углу 02. Как связан вектор г с векторами а и п? На рис. 4.14, б показано разложение вектора а на две составляющие"opengl1_234.html">⇐ Предыдущая| |Следующая ⇒