Векторное произведение (cross product, или vector product) двух векторов - это тоже вектор. Оно имеет много полезных свойств, но здесь мы чаще всего будем использовать то, что оно перпендикулярно к обоим исходным векторам. Векторное произведение определено только для трехмерных векторов.
Для трехмерных векторов а - (ах, ау, аг) и b - (b^ by, Ьг) векторное произведение обозначается а х Ь. В терминах стандартных единичных векторов i, j и к (см. равенство 4.18) оно записывается так: а х Ь = (ауЬг - aby)i + (агЬх - ахЬг)) + (axby - ауЬх)к. (4.28)
(На самом деле векторное произведение может быть выведено из более фундаментальных принципов, как это делается в упражнениях.) Поскольку вышеприведенная форма достаточно трудна для запоминания, векторное произведение часто записывают в виде легко запоминаемого определителя:
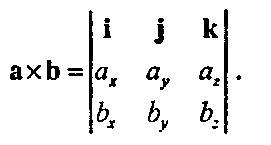
(4.29)(В приложении Б приведен обзор определителей.) Таким образом, для запоминания структуры векторного произведения достаточно запомнить, как сформирован этот определитель.
Пример 4.4.1
Непосредственное вычисление векторного произведения векторов а = (3,0,2) и Ь = (4,1,8) дает а х Ь = = -2і - 16} + Зк. Чему равно Ь х а?
Векторные инструменты для графики
Из равенства (4.29) можно легко увидеть, что векторное произведение обладает следующими алгебраическими свойствами: Все эти равенства справедливы как для левосторонней, так и для правосторонней систем координат. Отметим последовательный (по алфавиту) порядок следования векторов в выражении \ х j - к, в котором содержится удобный мнемонический прием для запоминания направления векторных произведений.
Практические упражнения
4.4.1. Демонстрация четырех свойств Проверьте каждое из четырех вышеприведенных свойств векторного произведения.
4.4.2. Выведение векторного произведения Форма векторного произведения, приведенная в равенстве (4.28) в качестве его определения, на самом деле может быть выведена из более общих соображений. Мы должны только предположить, что: О Операция векторного произведения линейна.
О Векторное произведение вектора на самого себя равно нулю.
