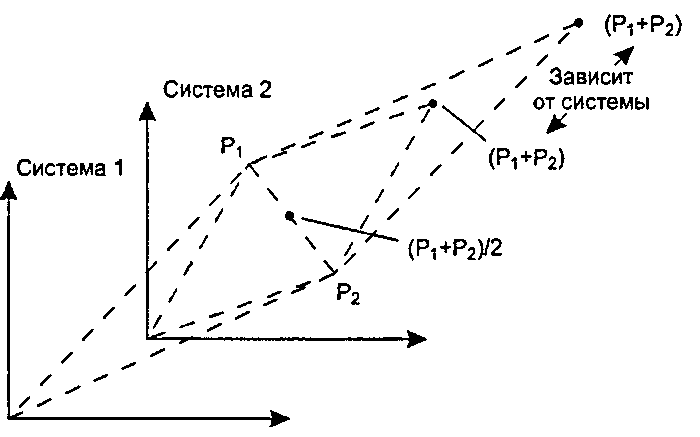
Рис. 4.19. Сложение точек - недопустимая операция Неудачный исход простой операции суммирования Р, + Р2, которая не приводит к тому, чтобы результат также был точкой, проиллюстрирован на рис. 4.19. Точки Р1 и Р2 показаны в двух системах координат, одна из которых смещена относительно другой. Рассматривая каждую точку как конец вектора, исходящего из начала координат, мы видим, что сумма Р, + Р2 дает в двух системах координат различные точки. Следовательно, Р, + Р2 зависит от выбора системы координат. Отметим для контраста, что аффинная комбинация 0,5(Р, + Р2) не зависит от такого выбора.

Точка плюс вектор - аффинная комбинация точек Существует другой способ изучения аффинных сумм точек, который интересен и сам по себе, а еще потому, что из него получается полезный инструмент для графики. Этот способ не требует использования однородных координат.

Овик Леонардович Мкртчян. перечень работ по ремонту автомобиля в автосервисе.

Рассмотрим формирование точки как смещение точки Л на вектор V, масштабированный скаляром г"opengl1_244.html">⇐ Предыдущая| |Следующая ⇒