Р = А + г(£-Л),

(4.36)

Р=?£ + (1 -г)Л,

(4.37)

1 Упоминание о тяжести возникло потому, что если тонкую пластину вырезать в форме треугольника Г и подвесить за нить, прикрепленную в центроиде, то пластина удержит равновесие. Сила тяжести действует во все стороны относительно центроида одинаково, поэтому пластина сбалансирована.

Векторные инструменты для графики

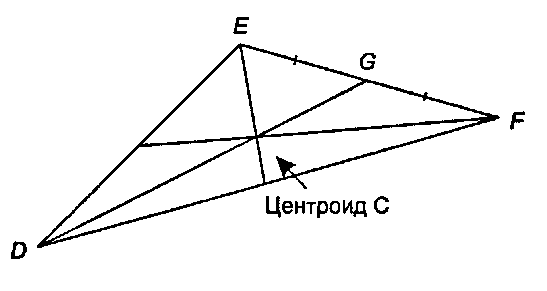
Рис. 4.20. Центр треугольника как аффинная комбинация По определению, медиана из точки И есть прямая, проведенная из вершины В в середину противоположной стороны. Тогда (7 - (Е + /г)/2. Прежде всего выясним, где находится точка, отмеряющая две трети расстояния от Б до С Применяя параметрическую форму, мы видим, что искомая точка должна иметь вид В + ((7 - где г - 2/3, что приводит к следующей аффинной комбинации"opengl1_245.html">⇐ Предыдущая| |Следующая ⇒