Рассмотрим общий случай составления линейной комбинации из m точек [Goldman, 85]: Зададимся вопросом, является ли Е точкой, вектором или ни тем, ни другим? Считая, что каждая точка Р. переместилась на вектор и, покажите, что Е «переместилась» в Е' = Е + 5и, где
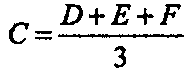
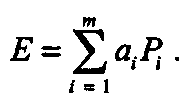
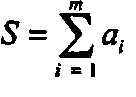
является суммой коэффициентов. Кроме того, покажите, что О Е является точкой, если 5=1. О Е является вектором, если 5 = 0. О Е не имеет смысла при других значениях 5.
4.5. Отображение ключевых геометрических объектов
4.5.3. Линейная интерполяция двух точек Аффинная комбинация точек, выраженная уравнением (4.36), а именно: Р = Л(1 -t) + Bt, выполняет линейную интерполяцию между точками А и В. Иными словами, дг-компонент Px(t) генерирует величину, которая составляет г-ю часть расстояния между точками Ах и Вх; аналогично для г/-компонента (в трехмерном случае и для z-компонента). Эта операция заслуживает присвоения имени, и для случая линейной интерполяции (linear interpolation) часто употребляется название lerpQ. Для одного измерения функция lerp(a, b, t) возвращает число, являющееся r-й частью на пути от а до Ь. В листинге 4.1 представлена простая реализация функции lerpQ: Листинг 4.1. Линейная интерполяция, осуществленная функцией 1егр()
float lerp(float a. float b. float t) {return a + (b - a) * t: // return a float // возвращаем вещественное число }
Подобным образом часто вычисляется точка Р(г), которая является г-й частью на пути по прямой линии от Л и В. Такую точку часто называют «твином» («tween» от слова «in-bet\veen» - промежуток) точек Л и В в (момент) г. Каждый компонент результирующей точки формируется как lerpO соответствующих компонентов точек Л и В. Для выполнения «твининга» («tweening») легко может быть написана (как?) процедура
Point2 Canvas:: Tween(Point2 A. Point2 В. float t) // tween A and В // твин А и В
Трехмерная версия почти не отличается от этой. Пример 4.5.2
Пусть Л = (4, 9) и В - (3, 7). В этом случае функция Tween(A, В, t) возвращает точку (4-t. 9-2t), aTween(A. В. 0.4) возвращает (3.6. 8.2). (Проверьте это на миллиметровке.)
