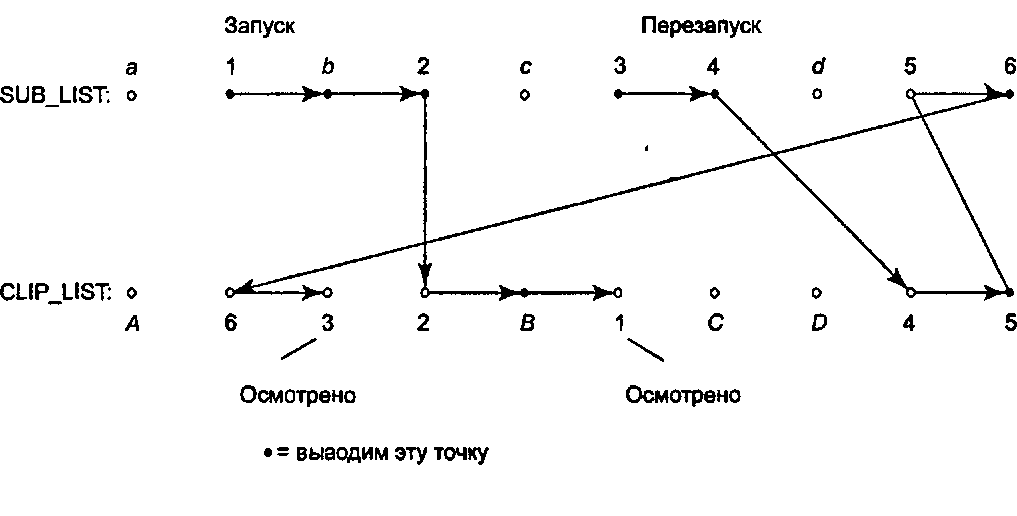
Рис 4.56. Приложение метода Вейлера-Азертона Пример более сложных полигонов, содержащих отверстия, показан на рис. 4.57. Те вершины, которые описывают отверстия, также вносятся в список в таком порядке, чтобы внутренняя часть полигона располагалась справа от ребра. (В случае отверстий это можно назвать порядком «против часовой стрелки».) Применяется то же правило, что и раньше"images/tmp8E4A-241.png" alt="Отсечение Вейлера-Азертона">
Рис 4.57. Отсечение Вейлера-Азертона: полигоны с отверстиями Тематическое задание 4.8. Булевы операции с полигонами Уровень сложности III.
Если рассмотреть полигон как множество точек (множество всех точек на границе или во внутренней части полигона), то результатом операции отсечения Вейлера-Азертона будет пересечение (intersection) двух полигонов - множество всех точек, принадлежащих обоим полигонам: CLIP и SUBJ. Полигоны на выходе алгоритма Вейлера-Азертона состоят из точек, лежащих одновременно внутри CLIP и исходного полигона SUBJ. В этом тематическом задании мы перейдем от пересечений к более общим теоретико-множественным операциям с полигонами, которые часто называют «булевыми» («Boolean») операциями. Потребность в таких операциях часто возникает и при моделировании [Mortenson, 85], и в графике (см. главу 14). В общем случае для двух множеств точек А и В определены следующие три теоретико-множественные операции:
купить трехкомнатную квартиру в новостройке в Геленджике. Больничные кровати в аренду www.qmeding.ru.