1 Как мы увидим позже, параллелепипед является трехмерным аналогом параллелограмма: шесть его сторон являются попарно параллельными гранями.
преобразования объектов
тате преобразования, будем рассматривать сетку как «несущую с собой» любые объекты, которые в ней определены. Это все, что способно сделать аффинное преобразование: исказить рисунки в той же мере, в какой одна сетка преображается в другую. Новые прямые могут быть наклонены под любым углом, они могут отстоять друг от друга на любое (одинаковое) расстояние, и две новые координатные оси не обязаны оставаться перпендикулярными. И, конечно, вся сетка может быть расположена в любом месте плоскости. Тот же результат имеет место и для трех измерений: все, что может сделать трехмерное аффинное преобразование, - это отобразить кубическую сетку в сетку из параллелепипедов.
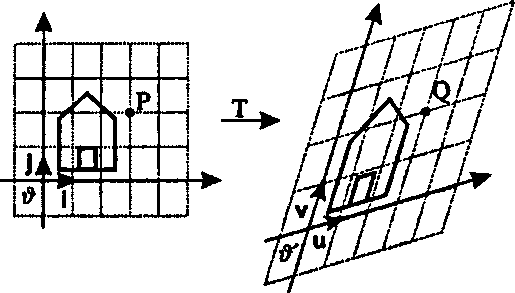
Рис 5.21. Преобразованная сетка Столбцы матрицы показывают преобразованный координатный фрейм Полезно подробно изучить столбцы матрицы М аффинного преобразования, поскольку они показывают, как преобразуется координатный фрейм. Пусть матрица М имеет следующий вид"images/tmp8E4A-286.png">
(5.21)так что столбцы этой матрицы равны соответственно ш,, пц и т3. Первые два столбца являются векторами (их третий компонент равен нулю), в то время как последний столбец является точкой (его третий компонент равен единице). Как всегда, интересующий нас координатный фрейм задается началом отсчета в и базисными векторами i и }, которые имеют следующие представления:
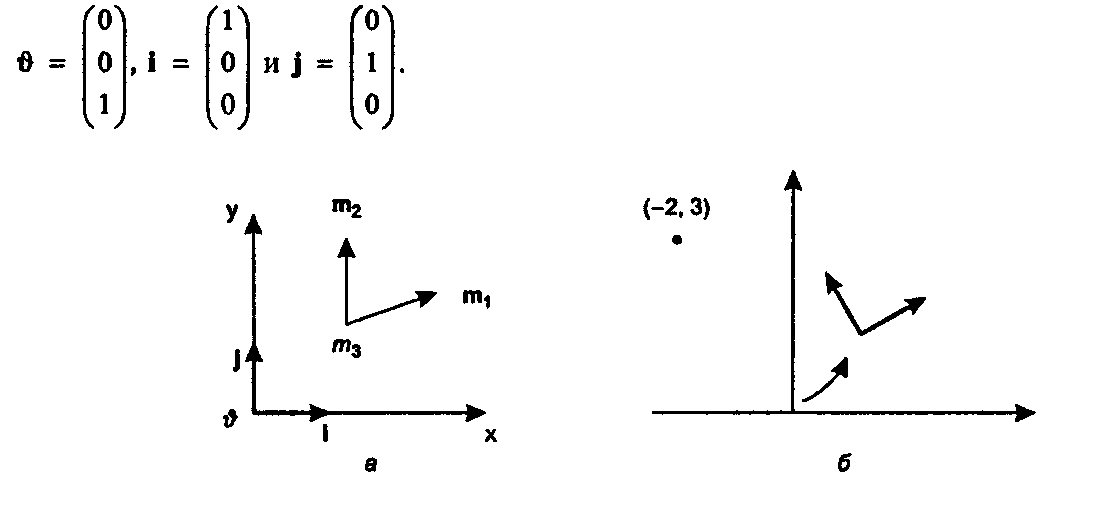
Рис 5.22. Преобразование формирует новый координатный фрейм Отметим, что вектор I преобразуется в вектор ш1 (проверьте это) согласно уравнению т, - М\,
5.2. Введение в преобразования аналогично вектор ] отображается в вектор т2, а начало отсчета * отображается в точку ту Эти отображения проиллюстрированы на рис. 5.22, а. Координатный фрейм (1, \, в) преобразуется в координатный фрейм (ш,, т2, т3), и эти новые объекты в точности являются столбцами матрицы преобразования.
Оси этого нового координатного фрейма не обязательно перпендикулярны, не обязаны они иметь и единичную длину. (Они сохраняют перпендикулярность, если преобразование включает в себя только повороты и равномерные масштабирования.) Любая точка Р = Рх1 + Р} + в преобразуется в точку 0, = Рхт1+ Рут2+ ту Иногда очень полезно взглянуть на матрицу аффинного преобразования с этой точки зрения.
