у А

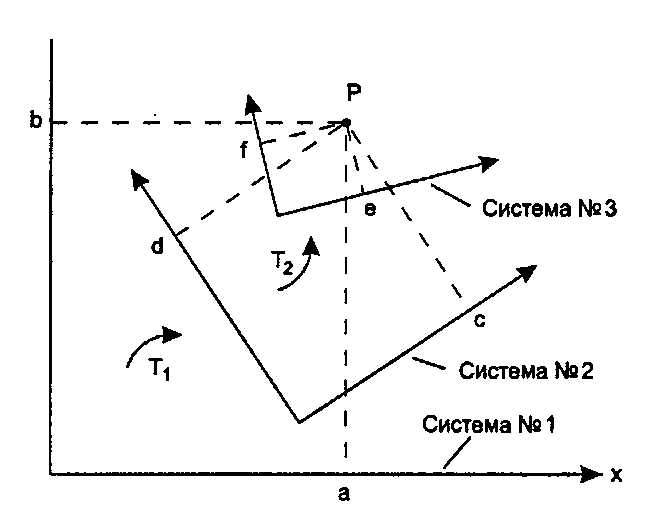
Рис. 5.32. Двукратное преобразование системы координат

Вопрос снова ставится так"images/tmp8E4A-315.png">

Преобразования объектов

Существенным является то обстоятельство, что при определении координат (а, Ь, 1)г из (e,f, 1)г первым применяется преобразование М2, а затем М,, то есть в обратном порядке по сравнению с тем, когда мы рассматривали применение преобразований к точкам. Обобщим вышесказанное на случай трех последовательных преобразований (после этого результат может быть обобщен на любое число преобразований).

Преобразование точек. Для того чтобы применить последовательность преобразований Т^.), Т2(.), Т3(.) (в указанном порядке) к точке Р, сформируем матрицу:

M-M3xM2xMv

Затем Р преобразуется в МР. Для составления каждого последующего преобразования M.t нужно умножить на него М.слева.

Преобразование системы координат. Для того чтобы применить последовательность преобразований Т^.), 7*2(.), Т3(.) (в указанном порядке) к точке Р, сформируем матрицу: М~ М{х.М2х.М3.

Таким образом, точка Р, выраженная в преобразованной системе, имеет в этой системе координаты МР. Для подключения каждого дополнительного преобразования Mi матрицу следует умножить на Mt справа.

Как работает OpenGL

В следующем разделе мы увидим, что в OpenGL имеются инструменты для последовательного применения преобразований и создания из них суммарного «текущего преобразования». Фактически OpenGL устроен так, что умножает справа каждую новую матрицу преобразования при компоновке их в суммарное преобразование. Поэтому разработчику модели часто представляется более естественным рассуждать в терминах последовательного преобразования системы координат, так как порядок, в котором эти преобразования выполняются, тот же, что и порядок, в котором их выполняет OpenGL.

⇐ Предыдущая| |Следующая ⇒