Практические упражнения
5.4.1. Связь между преобразованием системы координат и преобразованием точки Мы хотим проверить уравнение (5.35). Для того чтобы сделать это, докажите каждый из следующих пунктов: а) Покажите, что точка Р с координатами (с, d, 1)г в системе № 2 имеет представление ci' + dj' + f>'.
Доставка бутилированной воды архыз в офис. Доставка бутилированной питьевой воды в офис.
б) Мы хотим выяснить, где располагается точка Рв системе № 1. Покажите, что представление (в системе № 1) вектора ï равно М(1,0,0)г, вектора j' - М(0,1,0)г, а точки f>' - М(0,0,1).
в) Покажите, что представление точки ci' + dj' + f>' равно сМ(1,0,0)г + dM(0, 1, 0)г + М(0,0,1)г.
г) Покажите, что представление из пункта в) то же самое, что М(с, 0,0)г + М(0, d, 0)г + М(0, О, 1)г, и что оно равно М(с, d, 1)г, как утверждалось выше.
5.4.2. Использование элементарных примеров На рис. 5.33 показано действие четырех элементарных преобразований системы координат. В каждом случае исходная система с осями х и у преобразуется в новую систему с осями х' и у'.
а) На рис. 5.33, а показан результат перемещения на (яг, и). Покажите, что точка (е,/) в новой системе имеет координаты (e + m,f +п)ъ исходной системе.
б) На рис. 5.33, б показан результат поворота относительно начала координат на угол А градусов. Покажите, что точка (e,f) в новой системе имеет в старой системе координаты (ecos(a) -/sin(a), esin(a) + /cos(a)), где a - лЛ/180 радиан.
в) На рис. 5.33, в показан результат масштабирования осей на (3,2). Для наглядности новые и старые оси изображены слегка смещенными. Докажите, что точка (е,/) в новой системе имеет в старой системе координаты (Зе, 2/).
г) На рис. 5.33, г показан специальный случай масштабирования: отражение относительно оси х. Докажите, что точка (е, /) имеет в старой системе координаты (е, -/).
5.5. Использование аффинных преобразований в программах
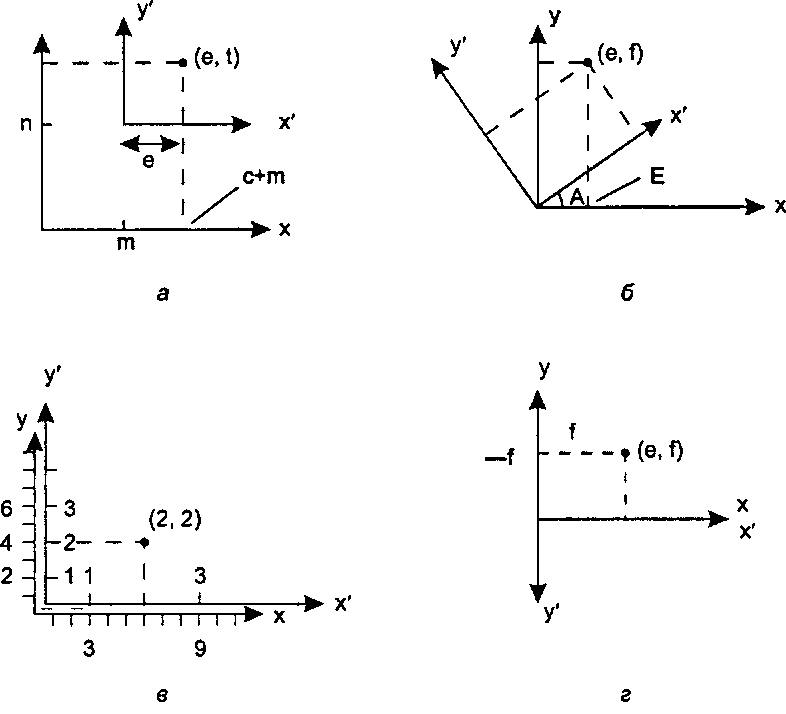
Рис. 5.33. Элементарные преобразования между системами координат: а) перемещение (т, п); 6) поворот (а); в) масштабирование с множителем (3, 2); г) масштабирование с множителем (1, -1)