Пример 5.8.1
(4 2
-3Ïна произведение матриц сдвига, масштабирования и поворота.
Разложите матрицу М -Решение Проверьте следующее выражение, полученное прямой подстановкой в уравнение (5.39): м =
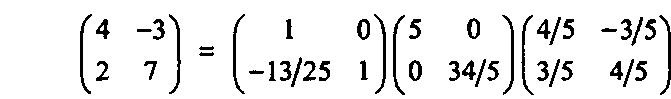
Двумерный поворот эквивалентен трем сдвигам Матрицы могут быть разложены различными способами. Фактически матрицу поворота можно записать в виде произведения трех матриц сдвига [РаеШ, 152]. Из этого следует особенно быстрый способ для выполнения серий поворотов.
5.8. Тематические задания Рассмотрим уравнение:
'cos(a) 51п(«)Л = Г1 tg(fl/2)V 1 OVl tg(a/2\ -sin(a) cos(a)J [о 1 J[-sin(a) 1 До 1 J'
представляющее поворот в виде трех последовательных сдвигов. Данное уравнение можно проверить непосредственным умножением. Оно показывает, что поворот является сдвигом вдоль оси у, за которым следует сдвиг по оси х, а затем повторение первого сдвига. Обозначьте Т= tg(a/2), 5 = sin(s) и покажите, что последовательность операций поворота точки (х, у) может быть записана следующим образом1: х' = Т*у + х, (первый сдвиг)
У' = У, х" - х\ (второй сдвиг)
y"-y'-S*x[;х' - Т*у" + х', (третий сдвиг) У"' = У", где штрихи использованы для того, чтобы отличить новые значения от старых. Однако операции вида х" - х'1 не делают ничего, поэтому штрихи здесь не нужны, и последовательность равенств выглядит короче: х = х + Т*у, у у- S*x, (фактические операции для выполнения трех сдвигов) х" х+.Т*у.
Если нам нужно выполнить только один поворот, то этот способ не дает выигрыша. Процесс, однако, становится более эффективным, если нам требуется выполнить целую последовательность поворотов на один и тот же угол. Это может понадобиться нам в двух типичных случаях:
1. При вычислении вершин и-угольника, которые являются точками, расположенными на равных расстояниях по окружности.
2. При вычислении точки вдоль дуги окружности.
Разработайте программу для вычисления положений п точек по окружности. Эта программа загружает последовательные значения (cos(2jri/n + b), sin(2ro/n + b)) в массив точек р[].
