Листинг 5.10. Программа быстрого рисования дуги
void drawArc2(RealPoint с. double R.
double startangle. double sweep) // in degrees II ъ градусах {
#define n 30
#define RadPerDeg .01745329
double delang - RadPerDeg * sweep / n:double T - tan(delang/2): // tan.of half angle // тангенс половинного угла
double S - 2 *T/(1 +T * T):продолжение &
Отметим, что ь\п(а) можно легко найти из tg(a/2) с помощью одного умножения и одного деления: 5 - (2Г)/(1 + Г2)-
Преобразования объектов
Листинг 5.10 (продолжение)
// sine of half angle // синус половинного угла
double snR =R * sintRadPerDeg * startangle):
double csR =R * costRadPerDeg * startangle):
moveTo(c.x + csR. c.y + snR):
for(int i - 1; i < n: i++)
{snR +- T * csR: // build next snR. csR pair // создаем следующую пару snR. csR
Купить воду с доставкой на дом недорого. Купить воду с доставкой на дом архыз. черников виктор викторович орел нарколог отзывы.
csR -- S * snR:
snR += T * csR:
lineTotc.x + csR. c.y + snR):
}В листинге 5.10 показано, как использовать сдвиги для создания программы быстрого рисования дуг. Она делает ту же самую работу, что функция drawArcO из главы 3, однако является значительно более эффективной, поскольку в ней нет повторных вычислений sin( ) и cos( ). Разработайте тестовую программу, использующую эту подпрограмму для рисования дуг. Сравните эффективность вашей программы с теми «рисовальщиками дуг», в которых каждая вершина вычисляется с помощью тригонометрии.
Является ли сдвиг «фундаментальным» преобразованием?
Иногда в литературе по графике можно прочитать, что фундаментальными элементарными преобразованиями являются поворот, масштабирование и перемещение; а сдвиги относятся к «гражданам второго сорта». В основе такого отношения лежит то обстоятельство, что любой сдвиг может быть разложен на комбинацию поворотов и масштабирований. Приводимое ниже равенство может быть проверено путем перемножения трех матриц правой части [Greene, 94]:
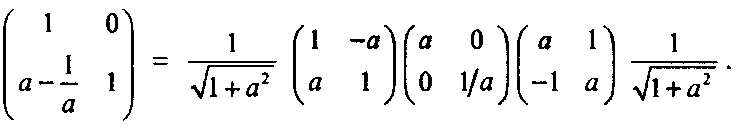
Средняя матрица является масштабированием, а обе крайние матрицы (вместе со своими масштабными множителями) ~ поворотами. Для левой матрицы поворота примем величину \/>Д + а2 равной косинусу, а величину -а]VI + а2 - синусу некоторого угла а. Тогда 1з(а) = -а. Для правой матрицы поворота также сопоставим аналогичные выражения с косинусом и синусом некоторого угла р\ тогда 1ё(3) = 1/а- Заметим, что углы а и 3 связаны соотношением: 3 = а + л/2. (Почему?)