1 В отечественной литературе - правильная призма имеет в качестве боковых граней прямоугольники. - Примеч. пер.

Моделирование поверхностей полигональными сетками

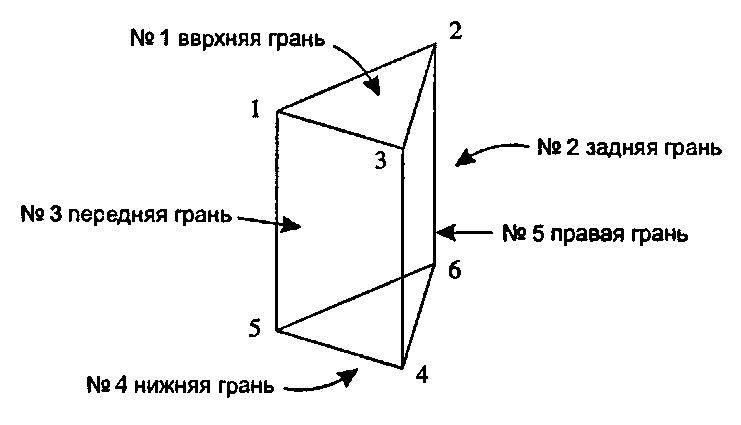
Рис. 6.16. Пример многогранного объекта

6.3.2. Приподнятый куб Составьте списки вершин, нормалей и граней для куба, одна из вершин которого располагается в точке (0,0, 0), а вершина, противоположная ей, - в точке (1,1,1).

6.3.3. Антипризма Постройте списки вершин, нормалей и граней для антипризмы, верхним полигоном которой является квадрат.

6.3.4. Определение связности сетки Является ли связной сетка, определенная следующим списком граней"box" rules="all" border="0">

Тело

V F

Е

Символ Шлефли

Тетраэдр

(3,3)

Гексаэдр

(4,3)

Октаэдр

(3,4)

Икосаэдр

(3, 5)

Додекаэдр

(5,3)

1 Названы в честь Платона (427-347 годы до н. э.), упоминавшего эти тела в своих Птаеиз. Однако они были известны и до Платона: игрушечный додекаэдр, найденный близ развалин Падуи, датируется 500 годом до и. э.

⇐ Предыдущая| |Следующая ⇒