6.3. Многогранники
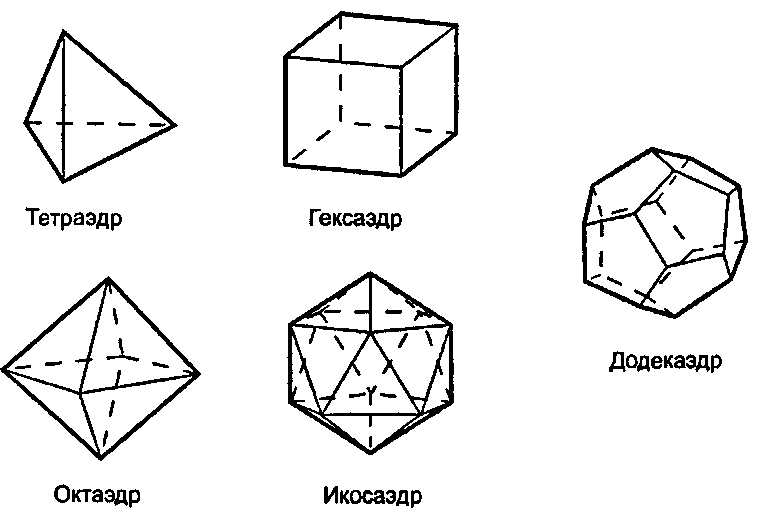
Рис. 6.17. Пять Платоновых тел Гранями трех Платоновых тел являются равносторонние треугольники, одно обладает квадратными гранями, а грани додекаэдра представляют собой пентагоны (пятиугольники). Куб является правильной призмой, а октаэдр - антипризмой. (Почему?) Значения величин V, F, Е для каждого из Платоновых тел приведены в табл. 6.4. Кроме того, там приводится и символ Шлефли1 (р, q) для каждого тела; он означает, что каждая грань является р-угольником и что q из них сходятся в каждой вершине.
Нетрудно построить сеточные списки для куба и октаэдра (см. упражнения 6.3.7,6.3.8). В этих упражнениях даются примеры списков вершин и граней для тетраэдра и икосаэдра и рассматривается способ составления списков нормалей. Кроме того, там показано, как вывести списки для додекаэдра из списков для икосаэдра, воспользовавшись «двойственностью» этих тел (это понятие мы также определим позднее).
Двойственные многогранники Каждому Платонову телу Р соответствует двойственный (dual) многогранник D. Вершинами полиэдра D являются центры граней полиэдра Р, так что ребра полиэдра D соединяют средние точки смежных граней полиэдра Р. На рис. 6.18 для каждого Платонова тела изображено вписанное в него двойственное тело. Ниже приводится список некоторых тел, являющихся двойственными.
О Двойственным для тетраэдра является также тетраэдр.
О Куб и октаэдр являются двойственными.
О Икосаэдр и додекаэдр также являются двойственными.
Двойственные многогранники имеют то же число ребер Е, а параметр Удля одного из них является параметром 5для другого. Кроме того, если (р, q) - символ Шлефли для одного из двойственных тел, то для второго символ Шлефли будет равен (q,p).
Если известен список вершин для одного Платонова тела Р, то легко создать такой же список для двойственного ему тела Д поскольку вершина k полиэдра D располагается в центре грани k полиэдра Р. Такой способ построения полиэдра D фактически создает многогранник, вписанный в многогранник Р.
Для того чтобы следить за нумерацией вершин и граней, мы используем модель (развертку), образуемую путем разрезания полиэдра вдоль определенных ребер и «разворачивания» его в плоскую фигуру таким образом, что все его грани видны с внешней стороны. Модели трех Платоновых тел показаны на рис. 6.19.
