quad-strip = {pvpl,pP…,pil^}. (6.9)

Предполагается, что вершины берутся парами, причем нечетные вершины формируют одно «ребро» полосы четырехугольников, а четные - другое ребро. Не каждый полигон можно представить в виде полосы четырехугольников. (Какие из полигонов, изображенных на рис. 6.31, не являются полосами четырехугольников? Какие печатные буквы алфавита могут быть нарисованы как полосы четырехугольников?)

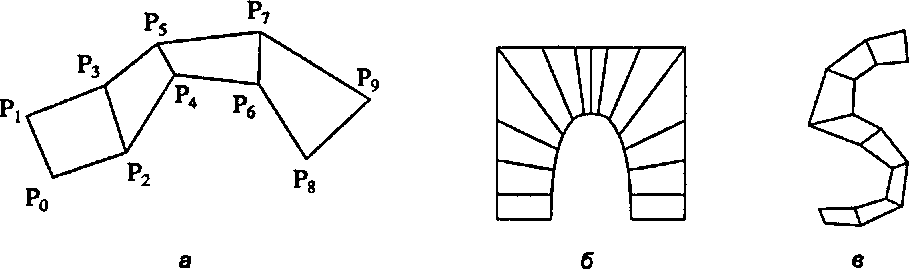
Рис. 6.32. Полосы четырехугольников и призмы, построенные на них

Когда сетка сформирована как экструзивная полоса четырехугольников, в список вершин помещается только 2М вершин, а в список граней помещаются только «внешние стенки». Всего имеется 2М - 2 граней. (Почему?) Следовательно, при визуализации сетки лишние стенки вообще не рисуются. Метод создания сетки для экструзивных полос четырехугольников будет принимать в качестве параметров массив двумерных точек и вектор экструзии"opengl1_408.html">⇐ Предыдущая| |Следующая ⇒