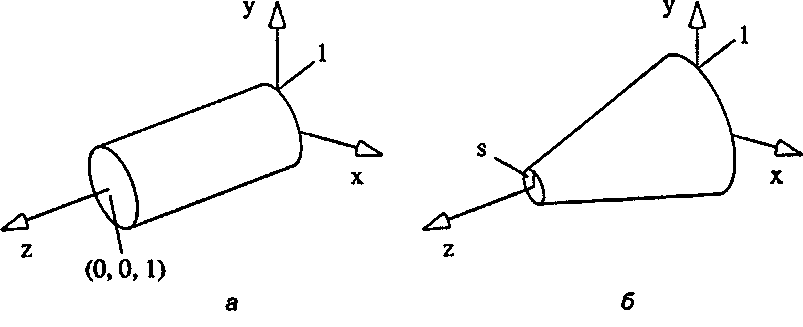
Рис. 6.47. Базовый цилиндр и конический цилиндр

Базовый цилиндр является частным случаем конического цилиндра при s = 1. Далее, базовый конус, который мы будем изучать следующим, также является частным случаем конического цилиндра при s - 0. Мы выведем формулы для конического цилиндра при произвольном значении параметра s, а положив s равным соответственно 1 или 0, из них можно будет получить формулы для базовых цилиндра и конуса.

Если рассматривать конический цилиндр как тонкую пустотелую «оболочку», то его боковая поверхность, или стенка (wall), будет задаваться неявной формой"opengl1_424.html">⇐ Предыдущая| |Следующая ⇒