Моделирование поверхностей полигональными сетками
Вообще говоря, не требуется, чтобы направление d было перпендикулярно к данной плоскости, однако если это имеет место, то данная поверхность называется прямым цилиндром (right cylinder). К этой категории принадлежит и базовый цилиндр. На рис. 6.53, б показан «ленточный» цилиндр, у которого кривая Ра(и) изгибается взад и вперед подобно ленте. Такая ленточная форма исследуется в упражнениях в конце раздела.
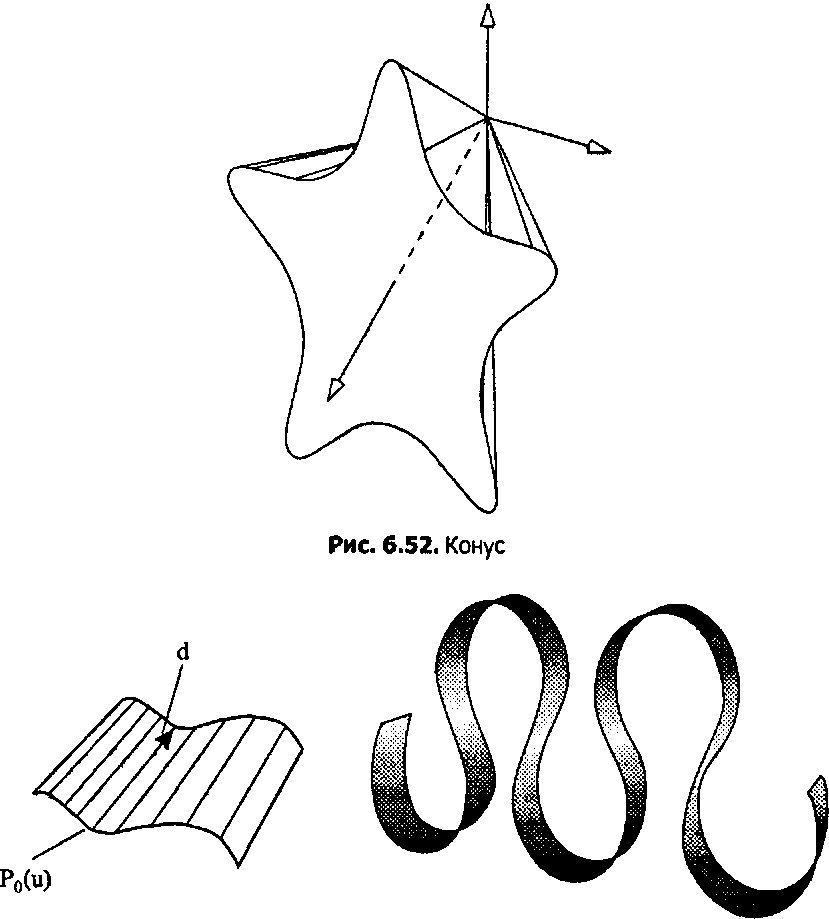
а 6
Рис, 6.53. Цилиндр (а); «ленточный» цилиндр (б)
Билинейные лоскуты
Билинейный лоскут получается в случае, когда обе кривые - Р0(и) и Р,(и) - являются отрезками прямых линий из одного и того же интервала для и, например от 0 до 1. Обозначим концевые точки кривой Р0(и) через Р00 и Р01 (в этом случае Р0(и) имеет вид (1 - и) Р00 + иР01), а концевые точки кривой Р,(и) - через Р10 и РИ. Тогда из равенства (6.35) следует, что данный лоскут имеет следующую параметрическую форму: Р(и, о) - (1 - о)(1 - и)Рю + (1 - о) uP0i + v(l - u)Pi0 + uvPu. (6.38)
Такая поверхность называется билинейной, потому что она линейно зависит от а и ». Билинейные лоскуты не обязаны быть плоскими; в действительности они являются плоскими, только если прямые Р0(и) и Р,(и) располагаются в одной и той же плоскости (см. упражнения ниже). В противном случае поверхность должна изгибаться по мере того, как мы перемещаемся от одной определяющей прямой к другой.
6.5. Каркасные аппроксимации гладких объектов Пример неплоского билинейного лоскута приведен на рис. 6.54. Прямая Р0(и) идет от точки (2, -2, 2) до точки (2, 2, -2), а прямая Р,(и) - от точки (-2, -2, -2) до точки (-2, 2, 2).
Эти прямые не являются компланарными; на рисунке показаны некоторые и-контуры, по которым ясно видно, как изгибается лоскут.
Нормальный вектор к билинейному лоскуту легко найти из уравнения (6.25). Если лоскут является плоским, то направление его нормали постоянно, однако ее длина может изменяться с изменением и и v. Если же лоскут не является плоским, то и величина, и направление его нормального вектора зависят от его расположения.
