Рис. 6.54. Билинейный лоскут

Моделирование поверхностей полигональными сетками

Рис. 6.57. Комбинирование лоскутов для создания лоскута Кунса

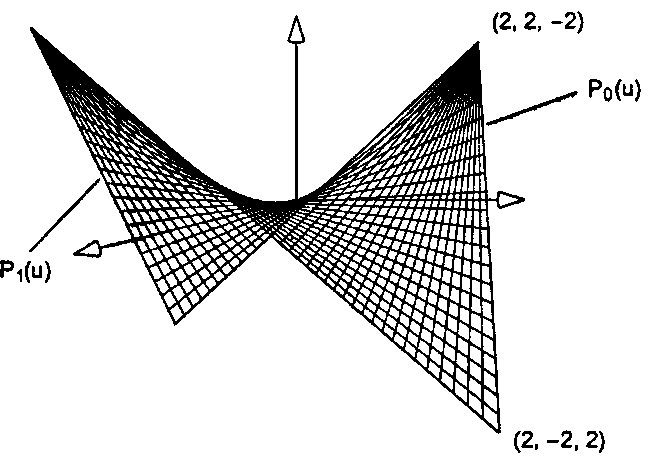
6.5. Каркасные аппроксимации гладких объектов Тогда формула для данного лоскута имеет виД"images/tmp8E4A-422.png" alt="Пример лоскута Кунса">

Рис. 6.58. Пример лоскута Кунса Практические упражнения

6.5.11. Пирамида - это конус

Какую форму будет иметь кривая Р,(и) для создания линейчатой поверхности, представляющей собой пирамиду с квадратным основанием? Получите такие выражения для кривой и точки Р0, чтобы квадратное основание пирамиды располагалось в плоскости xz, имело центр в начале координат и длины его сторон равнялись 2. Высота данной пирамиды должна равняться 1,5.

6.5.12. Ленточные цилиндры

Найдите параметрическую форму кривой Р0(и)> обеспечивающей хорошую аппроксимацию ленточного цилиндра, приведенного на рис. 6.53, б. Представьте, что эта лента обернута вокруг последовательности смежных круговых цилиндров единичного радиуса. Сентр i-ro цилиндра располагается в точке (х, у) = (i2d, ± г), где плюсы и минусы чередуются и d2 = 1 - г2. Выберите какое-либо значение г между 0 и 1.

6.5.13. Двойная спираль

Параметрическая форма спирали"opengl1_433.html">⇐ Предыдущая| |Следующая ⇒