n(u,v) = X(v)(z(v) cos (u),Z(v) sin (и), - X(v)), (6.41)
где точка означает первую производную функции. Масштабный множитель X(v) исчезает после нормирования вектора. Этот результат относится к формам, которые мы нашли для простых базовых поверхностей (см. упражнения ниже).
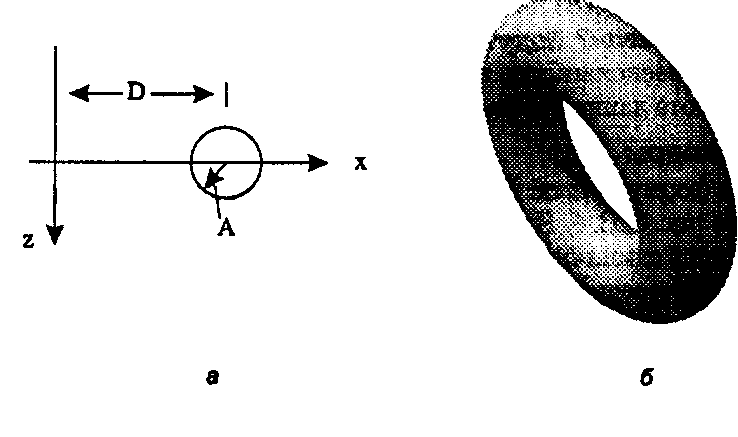
Рис. 6.59. Тор
Например, тор ^огш) получается путем развертки смещенной окружности вокруг оси г, как показано на рис. 6.59, а. Эта окружность имеет радиус А и смещена вдоль оси д; на расстояние Д следовательно, ее профиль С(р) = ф + Асо$&), Аът(х))). Тогда формула для тора (рис. 6.59, б) имеет следующий вид"images/tmp8E4A-424.png" alt="Поверхность вращения - купол Тадж Махала">
Рис. 6.60. Поверхность вращения - купол Тадж Махала На рис. 6.60, а приведен пример, в котором сделана попытка моделирования купола изящного храма Тадж Махал (Taj Mahal) в Агре, Индия. На рис. 6.60, б изображена профильная кривая в плоскости xz, а на рис. 6.60, в показана результирующая поверхность вращения. Этот профиль описывается множеством точек данных Ct = (Xit Z), поскольку не нашлось ни одной подходящей параметрической формулы. (Мы исправим этот недостаток в главе 11 и применим В-сплайн (B-spline) для создания гладкой параметрической кривой на базе множества точек данных.)
