11.6.2. Покажите, что смещения д(.)дают в сумме единицу при любом t
Рассмотрим сумму смещений: g(t) + g(t - 1) + g(t - 2), где g(t) - кусочный полином, определяемый уравнением (11.49). Покажите, что эта сумма равна единице для всех значений t в диапазоне от 2 до 3.
11.6.3. Являются ли полиномы Бернштейна сплайнами?
Покажите, что полиномы Бернштейна Вк1 (?) действительно являются сплайнами. Сколько кусочных полиномов соединяются для формирования каждого из них? Где находятся узлы? Какова степень этого сплайна? Обладает ли он достаточной непрерывной дифференцируемостью?
11.6.4. Потренируйте интуицию на квадратичных сплайнах
Задайте в каком-нибудь сложном порядке 12 контрольных точек, после чего нарисуйте кривую, сгенерированную с помощью квадратичных сплайн-функций из уравнения (11.49). Используйте то обстоятельство, что эта кривая проходит через середины определенных ребер контрольного полигона.
11.6.5. Построение замкнутых кривых без дополнительных контрольных точек Покажите, что уравнение (11.52) с небольшими изменениями, а именно создает замкнутую кривую на базе семи (различных) контрольных точек при изменении г от 0 до 7. Никаких дополнительных точек не требуется. Функция mod («целое число по модулю») эффективно «свертывает» стыковочные функции к интервалу [0,7], активизируя их на различных участках этого интервала. Для того чтобы увидеть, как это работает, нарисуйте для 1 = 4 пять функций g((£ - k) mod (I + 1)) для k - 0,1,2,3,4 при изменении г от 0 до 5.
порядка?
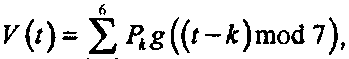
(11.53)Создание кривых и поверхностей
11.6.5. Сплайны и базисные функции Метод, включающий в себя смещение квадратичных полиномов g(t), похоже, предоставляет в наше распоряжение неплохое средство создания кривых. Поэтому стоит ли идти дальше? Проблема заключается в том, что нам требуется больший контроль над формой кривой: она должна больше «изгибаться» и быть более гладкой, чем 1-гладкая кривая. Такое требование предполагает переход к кубическим полиномам. Мы также хотим, чтобы дизайнер имел возможность указывать, какие контрольные точки должны интерполироваться. И было бы хорошо иметь единый алгоритм, который осуществлял бы все вышеописанные технологии дизайна, в том числе кривые Безье.
