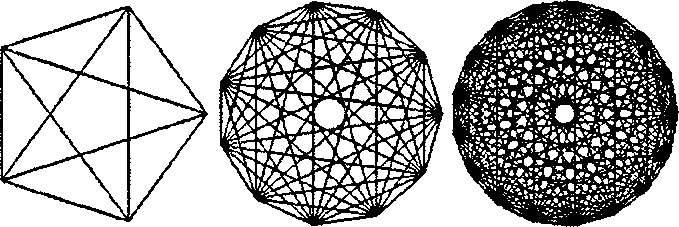
Рис. 3.34. 5-, 11- и 17-розетки Рисовать розетки легко - просто соедините каждую вершину со всеми остальными. Псевдокод для рисования розетки выглядит так"images/tmp8E4A-118.png">
а б Рис. 3.35.5-розетка и бесконечная регрессия пентагонов и пентаграмм Пример 3.6.3. Фигуры, основанные на двух концентрических п-угольниках
На рис. 3.36 изображено несколько форм, построенных на двух концентрических порождающих окружностях: внешней с радиусом /? и внутренней с радиусом //?, где / - некоторая дробь. В каждой фигуре используется разновидность и-угольника, величина радиуса которого находится между внутренним и внешним радиусами. Части а) и б) рисунка представляют собой известные логотипы компаний на базе 6-угольника и 10-уголышка. Фигура в) построена на 14-угольнике, а на рисунке г) показан в явном виде вписанный круг.

аба г Рис. 3.36. Семейство знаменитых логотипов
3.6. Фигуры на основе правильных многоугольников Практические упражнения
3.6.1. Звездчатые формы и розетки Пентаграмма рисуется путем соединения каждой второй точки при обходе пентагона. Обобщите данную схему на произвольный я-угольник с нечетным числом сторон и разработайте подпрограмму, рисующую этот так называемый «звездчатый многоугольник». Можно ли осуществить такую процедуру, используя единственную начальную команду moveToO, за которой следуют только команды ІіпеТоО (то есть без единого «поднятия пера»)? Что произойдет, если я четное?
